دائرة داخلية
(بالتحويل من مركز الدائرة المحاطة بالمثلث)
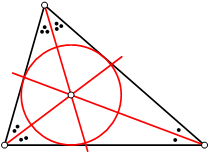
دائرة المثلث الداخلية هي دائرة تمس جميع أضلاعه من الداخل. ويُعرف مركزها بأنه النقطة الناتجة عن تقاطع منصفات زوايا المثلث، ويُرمز إليه بـ. بإسقاط هذه النقطة عمودياً على أحد الأضلاع يتشكل بذلك شعاع الدائرة الداخلية.[1]
خصائص مركز الدائرة الداخلية
عدل- تشكل هذه النقطة مع أحد رؤوس المثلث والمسقطين العموديين للمركز الداخلي على الضلعين التابعين لرأس المثلث المختار أربعة نقط دائرية.
برهان
ليكن ABC مثلثاً، والنقطتان D و E هما المسقطان العموديان لمركز الدائرة الداخلية I على الضلعين AC و AB على التوالي.
- إن المثلث IAD قائم الزاوية في النقطة D.
- إن المثلث IAE قائم الزاوية في النقطة E.
إذن ومنه الرباعي ADIE دائري
- تقسم هذه النقطة المثلث إلى 3 أزواج من المثلثات المتطابقة. كُل مثلثين يُشكلان شكل طائرة ورقية.
برهان
ليكن ABC مثلث نضع D و E المسقطين العموديين لمركز الدائرة الداخلية I على الضلعين AC و AB على التوالي.
- نعلم أن المثلث IAD قائم الزاوية في النقطة D.
- ونعلم أن المثلث IAE قائم الزاوية في النقطة E.
- وأن IE و ID شعاعي الدائرة.
- وكذلك المثلثين AEI و ADI يتشاركان في الضلع AI.
.ومنه نستنتج أن:
- الزاويتين المقابلتين للضلع AI متقايستين.
- وأن IE=ID
وبالتالي المثلثين ADI و AEI متشابهين وبالقياس على هذين المثلثين نستنتج أن مركز الدائرة الداخلي I يقسم المثلث ABC إلى ستة مثلثات متقايسة مثنى مثنى.
