مكعب رباعي الأبعاد
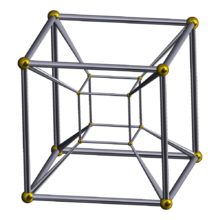
في علم الهندسة، المكعب رباعي الأبعاد أو المكعب رباعي البعد[1] أو المكعب الفائق رباعي الأبعاد (بالإنجليزية: Tesseract) هو النظير رباعي الأبعاد للمكعب.[2][3] التسراكت بالنسبة للمكعب مثل المكعب بالنسبة للمربع. كما أن سطح المكعب يتكون من 6 وجوه مربعة، فالسطح الفوقي للتسراكت يتكون من 8 خلايا مكعبة. تسراكت هي واحدة من ستة متعددات الجوانب الرباعية المنتظمة المحدبة.
| صنف فرعي من | |
|---|---|
| اختار الاسم |
تشارلز هوارد هينتون (1888) |
| يدرسه | |
| تعريف الصيغة | |
| الرموز في الصيغة | |
| يقابل | |
| رمز شليفلي | |
| لديه شكل الرأس | |
| has facet polytope |
فمثلا المربع في البعد الأول يكون على شكل خط لأن البعد الأول يحتوي على الطول فقط لا يحتوي على العرض والارتفاع .
والمربع في البعد الثاني يكون على شكل مربع عادي لأن البعد الثاني هو وطن المربع فالمربع يتكون من طول وعرض والبعد الثاني أيضاً يتكون من طول وعرض
وفي البعد الثالث يكون على شكل مكعب! فالبعد الثالث يحتوي على طول وعرض بالإضافة إلى الارتفاع مما يؤدي إلى اضطرار المربع وإضافة بعد جديد وهو الارتفاع ليتحول بعد ذلك إلى مكعب.
مراجع
عدل- ^ معجم مصطلحات الرياضيات (بالعربية والإنجليزية)، القاهرة: مجمع اللغة العربية بالقاهرة، 2019، ص. 403، OCLC:1413794243، QID:Q125363697
- ^ Du Sautoy، Marcus. "A 4 Dimensional Cube in Paris". The Number Mysteries. مؤرشف من الأصل في 2016-01-14. اطلع عليه بتاريخ 2012-06-17.
- ^ "Unfolding an 8-cell". مؤرشف من الأصل في 2019-01-09.


