مخطط مزدوج
المخطط المزدوج أو الرسم البياني الثنائي (بالإنجليزية: Dual graph) يمثل مخططاً أو رسمة لمخطط مستوٍ G، بحيث تكون لديه عقدة لكل وجه في المستوي G وذلك كما هو موضح في فرع نظرية المخططات من علم الرياضيات. يحتوي المخطط المزدوج على ضلع كلما تم فصل وجهين من المستوي G عن بعضهما البعض بضلع، وحلقة ذاتية عندما يظهر نفس الوجه على جانبي الضلع. وهكذا فإن كل ضلع e من المستوي G له ضلع مزدوج مقابل، ونقاط نهايتها هي العقد المزدوجة المقابلة للأوجه على جانبي الضلع e. يعتمد تعريف الازدواجية على اختيار تضمين المخطط G، لذا فهو خاصية للرسوم البيانية المستوية (الرسوم البيانية المضمنة بالفعل في المستوى) بدلاً من المخططات المستوية (الرسوم البيانية التي قد تكون مضمنة ولكن التضمين لها لم يعرف بعد). وبالنسبة إلى المخططات المستوية بشكل عام، قد يكون هناك العديد من المخططات المزدوجة، وذلك اعتمادًا على اختيار التضمين المستوي للمخطط.
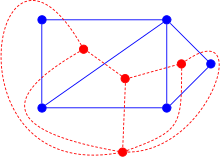
تاريخيًا كان أول شكل من أشكال ازدواجية الرسم البياني الذي تم الاعتراف به هو اتحاد المواد الصلبة الأفلاطونية في أزواج من متعددات الوجوه المزدوجة. وازدواجية المخطط البياني هي تعميم طوبولوجي للمفاهيم الهندسية متعددة السطوح والفسيفساء الثنائية، وهي بدورها معممة جبريًا من خلال مفهوم ماترويد المزدوج. وتتضمن الاختلافات في ازدواجية الرسم البياني المستوي نسخة من الازدواجية للرسوم البيانية الموجهة، وازدواجية الرسوم البيانية المضمنة في الأسطح ثنائية الأبعاد غير المستوية. ومع ذلك لا ينبغي الخلط بين هذه المفاهيم للمخططات المزدوجة وبين مفهوم مختلف للرسم البياني المزدوج من الضلع إلى العقدة أو الرسم البياني الخطي للمخطط.
يستخدم المصطلح مزدوج لأن خاصية كون المخطط مزدوج متماثلة، مما يعني أنه إذا كانت H زوج ثاني من المخطط المتصل G، فإن G هي ازدواج (ثنائية) لـH. فعند مناقشة ازدواجية المخطط G، يمكن الإشارة إلى الرسم البياني G نفسه باسم «المخطط الأولي». يمكن ترجمة العديد من خصائص وهياكل المخطط الأخرى إلى خصائص وهياكل طبيعية أخرى للثنائي المزدوج. على سبيل المثال الدورات الازدواجية لها هي قطع، والأشجار المتفرعة الازدواجية لها هي مع مكملات الأشجار المتفرعة، والمخططات البسيطة (بدون أضلاع متوازية أو حلقات ذاتية) الازدواجية لها هي مخطط 3 أضلاع متصلة (3-edge-connected graphs).
يمكن أن تساعد ازدواجية المخطط البياني في تفسير بنية المتاهات وأحواض الصرف. كما تم تطبيق المخططات المزدوجة في رؤية الحاسوب، والهندسة الحاسوبية، وتوليد الشبكات، وتصميم الدوائر المتكاملة.
أمثلة
عدلالدورات وثنائيات الأقطاب
عدليقسم التضمين المستوي الفريد للرسم البياني الدائري المستوى إلى منطقتين فقط، داخل وخارج الدائرة وذلك من خلال نظرية منحنى جوردان. ومع ذلك في الدائرة رقم n يتم فصل هاتين المنطقتين عن بعضهما البعض بواسطة عدد n من الأضلع المختلفة. لذلك فإن الرسم البياني المزدوج للدائرة رقم n عبارة عن رسم بياني متعدد برأسين (مزدوجين في المناطق) متصلين ببعضهما البعض بواسطة عدد n من الأضلع المزدوجة. ويسمى هذا الرسم البياني الرسم البياني ثنائي القطب (Dipole graph). وعلى العكس من ذلك فإن المخطط المزدوج لعدد n من ضلع ثنائي القطب هو الدائرة رقم n.[1]
المجسم كثير السطوح المزدوج
عدلوفقًا لنظرية شتاينتس يجب أن يكون كل رسم بياني متعدد السطوح (الرسم البياني الذي يتكون من عُقد وأضلع مجسم ثلاثي الأبعاد محدب) مستويًا ومتصلًا بـ3 عقد، وكل رسم بياني مستوٍ متصل بـ 3 عقد يأتي من متعدد السطوح المحدب وبهذه الطريقة. وكل متعدد السطوح محدب ثلاثي الأبعاد له مجسم مزدوج. يحتوي متعدد السطوح المزدوج على عقدة لكل وجه من وجوه متعدد السطوح الأصلي، مع وجود عقدتين مزدوجين متجاورين عندما يتشارك الوجهان المقابلان في ضلع. وعندما يكون اثنان من متعددات الوجوه ثنائي، فإن الرسوم البيانية الخاصة بهم تكون ثنائية أيضًا. فعلى سبيل المثال تأتي المجسمات الأفلاطونية في أزواج مزدوجة مع ثنائي ثماني السطوح للمكعب، وثنائي الوجوه ثنائي لعشري الوجوه، ورباعي الوجوه مزدوجًا لنفسه.[2] ويمكن أيضًا توسيع ازدواجية متعدد الوجوه لتشمل ازدواجية متعدد الجوانب ذات أبعاد أعلى.[3] ولكن هذا الامتداد للازدواجية الهندسية ليس له صلات واضحة بالازدواجية النظرية للرسم البياني.
المخطط المزدوج الذاتي
عدليُقال إن الرسم البياني المستوي يكون مزدوجًا ذاتيًا إذا كان متماثلًا مع مخططه المزدوج. وتوفر الرسوم البيانية للعجلة عائلة لا حصر لها من الرسوم البيانية المزدوجة الذاتية القادمة من متعددات الوجوه الذاتية المزدوجة (الأهرامات).[4][5]
الخصائص
عدلتتوافق العديد من المفاهيم الطبيعية والمهمة في نظرية الرسم البياني مع مفاهيم طبيعية مساوية أخرى ولكن مختلفة في المخطط المزدوج. نظرًا لأن ثنائية ازدواجية المخطط المستوي المتصل تتشابه مع الرسم البياني الأولي،[6]
انظر أيضًا
عدلالمراجع
عدل- ^ van Lint، J. H.؛ Wilson، Richard Michael (1992)، A Course in Combinatorics، Cambridge University Press، ص. 411، ISBN:0-521-42260-4.
- ^ Bóna، Miklós (2006)، A walk through combinatorics (ط. 2nd)، World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ، ص. 276، DOI:10.1142/6177، ISBN:981-256-885-9، MR:2361255، مؤرشف من الأصل في 2016-05-01.
- ^ Ziegler، Günter M. (1995)، "2.3 Polarity"، Lectures on Polytopes، كتب دراسات عليا في الرياضيات، ج. 152، ص. 59–64.
- ^ إيريك ويستاين، Self-dual graph، ماثوورلد Mathworld (باللغة الإنكليزية).
- ^ Servatius، Brigitte؛ Christopher، Peter R. (1992)، "Construction of self-dual graphs"، The American Mathematical Monthly، ج. 99، ص. 153–158، DOI:10.2307/2324184، JSTOR:2324184، MR:1144356.
- ^ Nishizeki، Takao؛ Chiba، Norishige (2008)، Planar Graphs: Theory and Algorithms، Dover Books on Mathematics، Dover Publications، ص. 16، ISBN:978-0-486-46671-2، مؤرشف من الأصل في 2021-02-05.