دوران المحاور

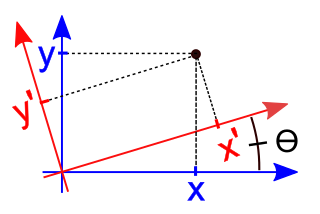
في الرياضيات، دوران المحاور عبارة عن رسم خرائط من نظام إحداثيات ديكارتي س ص إلى نظام إحداثيات x'y'-كارتيزي حيث يحتقظ بالأصل ثابتًا ويتم الحصول على محوري x' و y' عن طريق تدوير محاور x و y عكس اتجاه عقارب الساعة بزاوية $\theta$. النقطة P لها إحداثيات (x ,y) فيما يتعلق بالنظام الأصلي والإحداثيات (x ,'y’) فيما يتعلق بالنظام الجديد. في نظام الإحداثيات الجديد، ستظهر النقطة P وكأنها قد تم تدويرها في الاتجاه المعاكس، أي في اتجاه عقارب الساعة عبر الزاوية $\theta$. يتم تعريف دوران المحاور في أكثر من بعدين بالمثل. دوران المحاور هو خريطة خطية وتحويل جامد.

نظام إحداثيات x ,y

التحفيز

تعد أنظمة التنسيق ضرورية لدراسة معادلات المنحنيات باستخدام طرق الهندسة التحليلية. لاستخدام طريقة هندسة الإحداثيات، توضع المحاور في موضع مناسب فيما يتعلق بالمنحنى قيد الدراسة. على سبيل المثال، لدراسة معادلات القطوع الناقصة والقطع الزائدة، عادة ما توجد البؤر على أحد المحاور وتقع بشكل متماثل فيما يتعلق بالأصل. إذا كان منحنى (القطع الزائد، القطع المكافئ لا يقع، والقطع الناقص، وما إلى ذلك) بشكل ملائم فيما يتعلق محاور، يجب تغيير نظام الإحداثيات لوضع منحنى في موقع مناسب ومألوفة والتوجه. تسمى عملية إجراء هذا التغيير تحويل الإحداثيات.

يمكن تبسيط حلول العديد من المشكلات عن طريق تدوير محاور الإحداثيات للحصول على محاور جديدة من خلال نفس الأصل.

الاشتقاق

المعادلات التي تحدد التحول في بعدين، والتي تقوم بتدوير المحاور x ,y عكس اتجاه عقارب الساعة من خلال زاوية $\theta$ في محاور x ,'y' يتم اشتقاقها على النحو التالي.

في نظام x ,y النقطة P لها إحداثيات قطبية $(r,\alpha )$. بعد ذلك، في نظام x ,'y ' سيكون لدى P إحداثيات قطبية $(r,\alpha -\theta )$.

باستخدام الدوال المثلثية، لدينا

$x=r\cos \alpha$

(1)

$y=r\sin \alpha$

(2)

وباستخدام الصيغ المثلثية القياسية للاختلافات، لدينا

$x'=r\cos(\alpha -\theta )=r\cos \alpha \cos \theta +r\sin \alpha \sin \theta$

(3)

$y'=r\sin(\alpha -\theta )=r\sin \alpha \cos \theta -r\cos \alpha \sin \theta .$

(4)

استبدال المعادلتين ( 1 ) و ( 2 ) في المعادلتين ( 3 ) و ( 4 )، نحصل عليها

$x'=x\cos \theta +y\sin \theta$

(5)

$y'=-x\sin \theta +y\cos \theta .$

(6)

يمكن تمثيل المعادلتين ( 5 ) و ( 6 ) في شكل مصفوفة على النحو التالي

${\begin{pmatrix}x'\\y'\end{pmatrix}}={\begin{pmatrix}\cos \theta &\sin \theta \\-\sin \theta &\cos \theta \end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}},$

وهي معادلة المصفوفة القياسية لدوران المحاور في بعدين.

التحويل العكسي هو

$x=x'\cos \theta -y'\sin \theta$

(7)

$y=x'\sin \theta +y'\cos \theta ,$

(8)

أو

${\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{pmatrix}}{\begin{pmatrix}x'\\y'\end{pmatrix}}.$