نواس

النُّوَاس أو الرّقّاص أو البَنْدُول (بالإنجليزية: Pendulum)‏ جسم مرتبط بنقطة محورية ثابتة بخيط/حبل بحيث يستطيع أن يتحرك بحرية في مستوى واحد، من اليمين إلى اليسار. العالم الفرنسي ليون فوكو (1819-1868) هو مكتشف النواس.

رقاص

معلومات عامة

صنف فرعي من	هزاز توافقي
تعريف الصيغة	${\frac {d^{2}\theta }{dt^{2}}}+{\frac {g}{l}}\sin \theta =0$
الرموز في الصيغة	${\frac {d^{2}\theta }{dt^{2}}}$ $\sin$ $l$ $g$ $\theta$
له جزء أو أجزاء	خيط أو وتر pendulum bob (en) رابط ميكانيكي

  لمعانٍ أخرى، طالع نواس (توضيح).

  ميّز عن وصلة صفحة.

  لمعانٍ أخرى، طالع رقاص (توضيح).

النواس، تظهر السرعة (v) والتسارع (a)

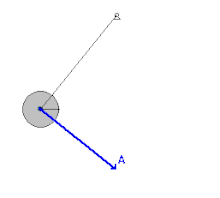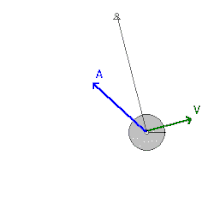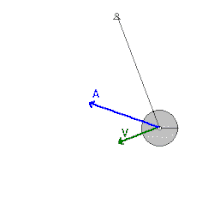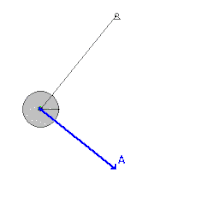
يقع الجسم تحت تأثير قوة الجاذبية التي تُسارعه إلى حين الوصول إلى حد أقصى على الناحية الأخرى فيتوقف لحظة. ثم تعيده قوة الجاذبية في إتجاه نقطة التوازن (أقل ارتفاع)، ولكن نظرًا لسرعته المكتسبة يتعدى نقطة التوازن. يتحرك نواس الساعة من نهاية عظمى يمنى إلى نهاية عظمى يسرى. يستغرق نواس الساعة بين النهاية العظمى اليمنى إلى النهاية العظمى اليسرى والعودة إلى النهاية العظمى اليمنى 1 ثانية. فيكون زمن دورته 1 ثانية. يعتمد زمن الدورة على طول النواس. فإذا كانت الساعة تؤخر وجب تقصير طول النواس، وإذا كانت الساعة تقدم وجب زيادة طول النواس.

تُطلق كلمة نُواس على ما تعلَّق وتدلى وتذبذب، وفِعلها ناس ينُوس نَوْساً ونَوَسَاناً أي تحرك وتذبذب متدلياً. وأبو نُوَاس كُنية الشاعر الحسن بن هانئ، لأنه كانت له ذؤابتان تنوسان على ظهره.

فترة دورة النواس تزيد مع ازدياد عرض الأرجحة

كيف تصنع نواساً

كل ما تحتاج لهذه التجربة هو نواس ساعة. ولصناعة النواس اربط ثقل في طرف خيط أو سلسلة خفيفة الوزن. الثقل ليس له وزن معين لكن لا تعلق عشرة كيلوجرامات مثلا على الخيط وأيضا لا تعلق ريشة عصفور. يكفي ثقل مناسب بين مئة إلى ثلاثمائة جرام لبناء النواس. وشيء آخر مهم في النواس ألا يكون الثقل مائلًا إلى أحد الجوانب عندما يتدلى من الخيط حتى لا يُحتك بالهواء. ومهم أيضًا ألا يبدأ الخيط بالدوران على نفسه عندما يتدلى منه الثقل. لتفادي ذلك استخدم سلسلة من النوع التي تكون مصنوعة من مجموعة كرات معدنية صغيرة (كرات معدنية وليس حلقات).

اختر للخيط أو السلسلة طولًا معينًا وقم بقياس الزمن الذي يستغرقه النواس للذهاب والعودة إلى نقطة البدء. تلك هي زمن الدورة. كرر القياس بعد زيادة طول السلسلة، وقس زمن الدورة تجد أن زمن الدورة يختلف باختلاف طول السلسلة.

طاقة الحركة وطاقة الوضع

المقالة الرئيسة: بقاء الطاقة

رسم متحرك لحركة النواس تظهر فيه نقطة السكون.

عندما يتحرك جسم في مجال كمجال الجاذبية الأرضية، وهذه هي حركة النواس، تكون مجموع طاقة الحركة وطاقة وضعه دائمًا ثابتة - ما دام لا يوجد احتكاك. فإذا رمزنا لطاقة حركة الجسم بالرمز K ورمزنا لطاقة وضعه بالرمز V، تنطبق المعادلة على حركة الجسم:

$E=K+V=constant$

في جميع الأوقات.

ونحسب طاقة الوضع لجسم من المعادلة:

$V=m.g.(h1-h0)$

حيث:

m كتلة الجسم بالكيلوجرام

g عجلة الجاذبية الأرضية: 9.81 متر/ثانية²

h1 ارتفاع الجسم عن الأرض عند النقطة العلوية (بالمتر)

h0 ارتفاع الجسم عن الأرض عند النقطة السفلى (بالمتر).

فإذا حسبنا تلك المعادلة حصلنا على مقدار طاقة وضعه بالكيلوغرام. متر²/ثانية ² . أو الجول.

وهما من وحدات الطاقة.

حساب طاقة الحركة

رأينا أعلاه كيف نستطيع حساب طاقة الوضع. نفترض كرة من الحديد كتلتها 1 كيلوغرام معلقة بحبل طوله 2 متر، ونفترض أن كتلة الحبل مهملة بالنسبة إلى كتلة الكرة الحديدية. نزيح الكرة المعلقة مسافة إلى الجانب بحيث ترتفع عن وضعها الأول (وضع السكون) 0.1 متر. من هذه المعلومات يمكننا حساب تغير طاقة وضع الكرة بتغير ارتفاعها، طبقًا للمعادلة:

$V=m.g.(h1-h0)$

بالتعويض عن تلك القيم نحصل على طاقة وضع الكرة عند أعلى نقطة على مسارها:

$V=1*9.8*0.1$

$V=0.98$ .. كيلوغرام . متر²/ثانية ²

من ناحية أخرى نعرف أن عند أعلى نقطة على مسار الكرة الدائري تكون طاقة حركة الكرة مساوية للصفر وتبدأ في الزيادة بالحركة في اتجاه نقطة السكون، وعندها تبلغ سرعة الكرة أعلى قدر لها. أي تكون طاقة وضع الكرة قد تحولت إلى أقصى طاقة حركة لها عند النقطة الوسطية (السفلى). إذن نستطيع كتابة المعادلة التي تعطي طاقة الحركة للكرة عند تلك النقطة، وهي:

$E_{k}={\begin{matrix}{\frac {1}{2}}\end{matrix}}mv^{2}$

أي أن طاقة حركة الكرة عند النقطة الوسطية تساوي:

$E_{k}={\begin{matrix}{\frac {1}{2}}\end{matrix}}mv^{2}=0.98$

والوحدة هنا أيضًا كيلوغرام . متر²/ثانية ²

ومنها نستطيع حساب السرعة القصوى v للكرة:

السرعة القصوى = 1.4 متر/الثانية

انظر أيضاً

• نواس بسيط
• نواس فوكو.
• الحركة التوافقية البسيطة.
• دورة (فيزياء).
• طاقة الوضع.
• طاقة حركية.
• مبدأ أقل طاقة.
• تسارع.