تشابك كمي
التشابك ظاهرة في الفيزياء الكمية، تحدث عندما يتولد زوجان أو مجموعة من الجسيمات أو تتفاعل أو تتشارك الجسيمات ذات القرب المكاني بحيث لا يمكن وصف الحالة الكمية لجسيم معين بشكل مستقل عن الجسيمات الأخرى، حتى لو فصلت مسافة كبيرة بين هذه الجسيمات.
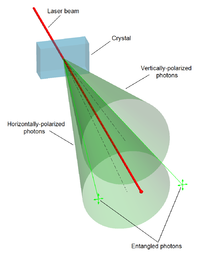
تُعد القياسات على الخصائص الفيزيائية مثل الموقع والزخم واللف المغزلي والاستقطاب المؤثرة على الجسيمات الكمومية مرتبطة بشكل مثالي. على سبيل المثال، إذا تولد زوجان من الجسيمات بطريقة كان فيها لفهما المغزلي الكلي صفرًا، وكان أحد الجسيمان يدور باتجاه عقارب الساعة على محور معين سيكون لف الجسيم الآخر عكس عقارب الساعة كما يُعتقد تمامًا بسبب تشابكهما. ومع ذلك، يسبب هذا السلوك آثارًا تناقضية، إذ إن أي قياس لخاصية جسيم تُمارِس تحولًا غير قابل للعكس على هذا الجسيم وستؤدي إلى تغير الحالة الكمومية الأصلية. في حالة الجسيمات المتشابكة، فإن هذا القياس سيُطبق على النظام ككل.
كانت هذه الظاهرة موضوعًا لورقة بحثية من إعداد ألبرت آينشتاين وبوريس بودولسكي وناثان روزن وأوراق بحثية أخرى من إعداد إرفين شرودينغر بعدهم بفترة قصيرة، وصفت تلك الأوراق البحثية ما يُعرف الآن بمفارقة آينشتاين-بودولسكي-روزن . اعتبر آينشتاين وآخرون أن هذا السلوك مستحيل، إذ يخرق هذا السلوك رؤية الواقعية المحلية لمبدأ السببية (وصفه آينشتاين على أنه فعل شبحي عن بعد) وحاججوا أن الصيغة المقبولة لميكانيك الكم ستكون غير كاملة لهذا السبب.
ومع ذلك، أُكِدَت التنبؤات الحدسية لميكانيك الكم، لاحقًا، تجريبيًا باختبارات قيس فيها اللف المغزلي والاستقطاب للجسيمات المتشابكة في مواقع منفصلة، خارقةً بشكل إحصائي مبدأ بل لعدم المساواة. في الاختبارات الأولية، لم يكن ممكنًا استبعاد أن نتيجة الاختبار في نقطة معينة انتقلت إلى نقطة البعيدة مؤثرةً على الناتج في الموقع الثاني. ومع ذلك، فاختبارات بِل المدعوة بأنها خالية الثغرات أجريت على مواقع منفصلة؛ يأخذ التواصل عند سرعة الضوء وقتًا أطول (في حالة معينة يكون أطول بعشرة آلاف ضعف) من الفترة بين القياسات.
وفقًا لبعض تفسيرات ميكانيكا الكم، فتأثير القياس يحدث بشكل آني، تجادل تفسيرات أخرى لميكانيكا الكم والتي لا تعترف بانهيار الدالة الموجية أنه لا يوجد تأثير على الإطلاق. ومع ذلك، تتوافق كل التفسيرات أن التشابك يُنشِئ توافقًا بين القياسات وأن المعلومات المتبادلة بين الجسيمات المتشابكة يمكن استغلالها ولكن أي انتقال للمعلومات في سرعات أكبر من سرعة الضوء يُعد أمرًا مستحيلًا.
أثبت التشابك الكمي تجريبيًا في الفوتونات والنيوترونات والإلكترونات والجزيئات الكبيرة بحجم كرة بوكي وحتى مع الماسات الصغيرة. نُقل عن علماء في جامعة غلاسكو في الثالث عشر من يوليو عام 2019 أنهم التقطوا أول صورة من نوعها لشكل قوي من التشابك الكمي المعروف باسم تشابك بل. يُعد استخدام التشابك في الاتصالات والحوسبة منطقةً نشطة للبحث.[1][2][3][4][5][6][7][8][9][10][11][12][13][14][15][16]
خلفية تاريخية
عدلنوقشت التنبؤات الحدسية لميكانيكا الكم حول النظم المرتبطة بشكل قوي أولًا من ألبرت آينشتاين عام 1935 في ورقة بحثية مشتركة مع بوريس بودولسكي وناثان روزن. أنشأ الثلاثة مفارقة آينشتاين-بودولسكي-روزن وهي تجربة احتمالية حاولت إظهار أن نظرية ميكانيكا الكم غير مكتملة. كتبوا في الورقة البحثية: «لهذا نحن مجبرون أن نستنتج أن توصيف ميكانيكا الكم للواقع الفيزيائي المعطى بالدوال الموجية غير مكتمل».
ومع ذلك، لم يخترع الثلاثة كلمة تشابك ولا عمموا الخصائص الخاصة للحالة التي درسوها. كتب شرودينغر، بعد ظهور ورقة إي بي آر (اختصار لأسماء العلماء الثلاثة)، رسالةً إلى آينشتاين بالألماني استخدم فيها كلمة Verschränkung الألمانية والتي ترجمها بنفسه إلى تشابك لوصف الارتباطات بين جسيمين يتفاعلان ومن ثم ينفصلان مثل الجسيمات الموجودة في تجربة إي بي آر.
نشر شروندينغر بعد فترة قصيرة ورقة تحدد وتناقش فكرة التشابك. أشار في الورقة إلى أهمية المفهوم وقال: «لن أدعوه ]التشابك[ السمة الواحدة بل هو السمة المميزة لميكانيكا الكم، وهي السمة التي تطبق انحرافها الكلي من خيوط الفكر الكلاسيكي».[17]
كان شرودينغر، مثل آينشتاين، غير راض عن مفهوم التشابك لأنه يخرق حد سرعة انتقال المعلومات المضمن في النظرية النسبية. تهكم آينشتاين لاحقًا من التشابك مُطلقًا عليه صفة فعل شبحي عن بعد.
ولدت ورقة إي بي آر البحثية اهتمامًا كبيرًا بين علماء الفيزياء وألهمت نقاشًا كثيرًا حول أسس نظرية ميكانيكا الكم (لعل أشهرها تفسير بوم لميكانيكا الكم)، ولكنها أنتجت أعمالًا منشورة أقل نسبيًا. بعيدًا عن الاهتمام، لم تُكتشف نقطة الضعف في حجة إي بي آر حتى عام 1964، عندما أثبت جون ستيوارت بل أن أحد افتراضاتهم الأساسية، وهو مبدأ المحلية المطبق على نوع تفسير المتغيرات المخفية لدى إي بي آر، كان متعارضًا رياضيًا مع تنبؤات نظرية الكم.
أظهر بل حدًا أعلى في مبدأ بل لعدم المساواة ينظر في قوة الارتباطات التي يمكن إنشاؤها في أي نظرية تخضع لمبدأ الواقعية المحلية وأظهر أن نظرية الكم تتنبأ بخروقات لهذا الحد لأنظمة متشابكة معينة. اختُبر مبدأه لعدم المساواة تجريبيًا وظهرت تجارب متوافقة كثيرة، بدايةً من العمل الرائد لستوارت فريدمان وجون كلاوسر عام 1972 وتجارب آلان آسبيكت عام 1982. حصل اختراق تجريبي بفضل كارل كوشير والذي قدم عام 1967 جهازًا يظهر فيه فوتونان منبعثان من ذرة كالسيوم متشابكين، وهي الحالة الأولى لتشابك الضوء المرئي. مر الفوتونان تمامًا من المستقبطات المتوزاية باحتمال أعلى مما كان يُتنبأ به كلاسيكيًا ولكن بارتباطات متفقة كموميًا مع حسابات مكيانيكيا الكم. وأظهر أيضًا أن الارتباط يختلف فقط بالنسبة (لجيب التمام المربع) للزاوية بين إعدادات المستقطب وينخفض بشكل أسي مع تأخر الزمن بين الفوتونات المنبعثة. استُخدم جهاز كوشر، بعد تجهيزه بمستقطبات أفضل، من فريدمان وكلاوسر، واللذان تمكنا من إثبات استقلال جيب التمام، واستخدماه لإظهار خرق مبدأ بل لعدم المساواة لعدة زوايا معدلة. أظهرت كل تلك التجارب توافقًا مع ميكانيكا الكم بدلًا من مبدأ الواقعية المحلية.[18]
على مدى عقود، ترك كل منهم ثغرةً واحدة على الأقل يمكن من خلالها التشكيك في صحة النتائج. ومع ذلك، أجريت تجربة عام 2015 أغلقت كل ثغرات الالتقاط والتحديد، وبشّرت بأن كلًا منهما خال من الثغرات؛ استبعدت تلك التجربة طبقة كبيرة من نظريات الواقعية المحلية بمبدأ التأكيد. يلاحظ آلان آسبكت أن ثغرة تحديد الاستقلال، والتي يُشير إليها على أنها بعيدة الاحتمال، ثغرة متبقية لا يمكن تجاهلها، ولم تُغلق بعد، وإن ثغرة الإرادة الحرة/الحتمية الفائقة غير قابلة للإغلاق. يقول آلان: «لا توجد تجربة مثالية كما هي، يمكن القول أنها خالية من الثغرات تمامًا».
يرى أقلية أنه على الرغم من صحة ميكانيكا الكم، لا يوجد فعل عن بعد آني أسرع من الضوء بين الجسيمات المتشابكة عندما تنفصل الجسيمات.
رفع عمل بل من احتمالية استخدام الارتباطات فائفة القوة بصفتها مصدرًا للاتصال. قاد عمله إلى اكتشاف بروتوكلات التوزيع الكمومي الأساسية، ولعل أشهرها البروتوكول بي بي 84 الذي اكتشفه تشارلز ه. بينيت وجيلي بريسارد، والبروتوكول إيه 91 الذي اكتشفه آرتور إيكيرت. على الرغم أن البروتوكول بي بي 84 لا يستخدم التشابك، يستخدم بروتوكول إيكريت خرق مبدأ بل لعدم المساواة بصفته إثباتًا للأمان.
قال علماء فيزياء في أكتوبر عام 2018 أن السلوك الكمومي قابل للشرح من خلال الفيزياء الكلاسيكية لجسيم واحد، ولكن ليس بالنسبة لعدة جسيمات مثلما يحدث في التشابك الكمومي وظاهرة عدم المحلية المرتبطة.
أعلن علماء فيزياء في يوليو عام 2019 أنهم التقطوا للمرة الأولى صورةً للتشابك الكمي.[19][20][21][22][23][24][25]
مراجع
عدل- ^ Einstein A, Podolsky B, Rosen N؛ Podolsky؛ Rosen (1935). "Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? WRONG PDF" (PDF). Phys. Rev. ج. 47 ع. 10: 777–780. Bibcode:1935PhRv...47..777E. DOI:10.1103/PhysRev.47.777. مؤرشف من الأصل (PDF) في 2020-01-09.
{{استشهاد بدورية محكمة}}: صيانة الاستشهاد: أسماء متعددة: قائمة المؤلفين (link) - ^ Schrödinger E (1935). "Discussion of probability relations between separated systems". Mathematical Proceedings of the Cambridge Philosophical Society. ج. 31 ع. 4: 555–563. Bibcode:1935PCPS...31..555S. DOI:10.1017/S0305004100013554.
- ^ Schrödinger E (1936). "Probability relations between separated systems". Mathematical Proceedings of the Cambridge Philosophical Society. ج. 32 ع. 3: 446–452. Bibcode:1936PCPS...32..446S. DOI:10.1017/S0305004100019137.
- ^ Yin، Juan؛ Cao، Yuan؛ Yong، Hai-Lin؛ Ren، Ji-Gang؛ Liang، Hao؛ Liao، Sheng-Kai؛ Zhou، Fei؛ Liu، Chang؛ Wu، Yu-Ping؛ Pan، Ge-Sheng؛ Li، Li؛ Liu، Nai-Le؛ Zhang، Qiang؛ Peng، Cheng-Zhi؛ Pan، Jian-Wei (2013). "Bounding the speed of 'spooky action at a distance". Physical Review Letters. ج. 110 ع. 26: 260407. arXiv:1303.0614. Bibcode:2013PhRvL.110z0407Y. DOI:10.1103/PhysRevLett.110.260407. PMID:23848853.
- ^ Matson، John (13 أغسطس 2012). "Quantum teleportation achieved over record distances". Nature News. DOI:10.1038/nature.2012.11163.
- ^ Francis, Matthew. Quantum entanglement shows that reality can't be local, Ars Technica, 30 October 2012 نسخة محفوظة 25 يوليو 2019 على موقع واي باك مشين.
- ^ روجر بنروز, The Road to Reality: A Complete Guide to the Laws of the Universe, London, 2004, p. 603.
- ^ Griffiths, David J. (2004)، Introduction to Quantum Mechanics (2nd ed.)، Prentice Hall، ISBN:978-0-13-111892-8
- ^ Kocher، CA؛ Commins، ED (1967). "Polarization Correlation of Photons Emitted in an Atomic Cascade". Physical Review Letters. ج. 18 ع. 15: 575–577. DOI:10.1103/PhysRevLett.18.575.
- ^ Carl A. Kocher, Ph.D. Thesis (University of California at Berkeley, 1967). Polarization Correlation of Photons Emitted in an Atomic Cascade نسخة محفوظة 8 نوفمبر 2019 على موقع واي باك مشين.
- ^ Kocher، CA (1971). "Time correlations in the detection of successively emitted photons". Annals of Physics. ج. 65 ع. 1: 1–18. DOI:10.1016/0003-4916(71)90159-X.
- ^ Kwiat، PG؛ Mattle، K؛ Weinfurter، H؛ Zeilinger، A؛ Sergienko، AV؛ Shih، Y (1995). "New High-Intensity Source of Polarization-Entangled Photon Pairs". Physical Review Letters. ج. 75 ع. 24: 4337–4341. Bibcode:1995PhRvL..75.4337K. DOI:10.1103/PhysRevLett.75.4337. PMID:10059884.
- ^ Zhao، Z؛ Chen، YA؛ Zhang، AN؛ Yang، T؛ Briegel، HJ؛ Pan، JW (يوليو 2004). "Experimental demonstration of five-photon entanglement and open-destination teleportation". Nature. ج. 430 ع. 6995: 54–58. arXiv:quant-ph/0402096. Bibcode:2004Natur.430...54Z. DOI:10.1038/nature02643. PMID:15229594.
- ^ Lu، Chao-Yang (2007). "Experimental entanglement of six photons in graph states". Nature Physics. ج. 3 ع. 2: 91–95. arXiv:quant-ph/0609130. Bibcode:2007NatPh...3...91L. DOI:10.1038/nphys507.
- ^ Yao، Xing-Can (2012). "Observation of eight-photon entanglement". Nature Photonics. ج. 6 ع. 4: 225–228. arXiv:1105.6318. Bibcode:2012NaPho...6..225Y. DOI:10.1038/nphoton.2011.354.
- ^ J. A. Formaggio, D. I. Kaiser, M. M. Murskyj, and T. E. Weiss (2016), "Violation of the Leggett-Garg inequality in neutrino oscillations". Phys. Rev. Lett. Accepted 23 June 2016. نسخة محفوظة 13 مارس 2020 على موقع واي باك مشين. [وصلة مكسورة]
- ^ Kumar, M., Quantum, Icon Books, 2009, p. 313.
- ^ Alisa Bokulich, Gregg Jaeger, Philosophy of Quantum Information and Entanglement, Cambridge University Press, 2010, xv.
- ^ J. S. Bell (1964). "On the Einstein-Poldolsky-Rosen paradox". Physics. ج. 1 ع. 3: 195–200. DOI:10.1103/PhysicsPhysiqueFizika.1.195.
- ^ Freedman، Stuart J.؛ Clauser، John F. (1972). "Experimental Test of Local Hidden-Variable Theories". Physical Review Letters. ج. 28 ع. 14: 938–941. Bibcode:1972PhRvL..28..938F. DOI:10.1103/PhysRevLett.28.938. مؤرشف من الأصل في 2019-11-13.
- ^ Sanctuary، B. C (2006). "Correlations in Entangled States". International Journal of Modern Physics B. ج. 20 ع. 11n13: 1496–1503. arXiv:quant-ph/0508238. DOI:10.1142/S0217979206034078.
- ^ Yin، Juan؛ Cao، Yuan؛ Yong، Hai-Lin؛ Ren، Ji-Gang؛ Liang، Hao؛ Liao، Sheng-Kai؛ Zhou، Fei؛ Liu، Chang؛ Wu، Yu-Ping؛ Pan، Ge-Sheng؛ Zhang، Qiang؛ Peng، Cheng-Zhi؛ Pan، Jian-Wei (2004). "The Statistical Interpretation of Entangled States". arXiv:quant-ph/0404011.
{{استشهاد بأرخايف}}: الوسيط|arxiv=مطلوب (مساعدة) - ^ Yin، Juan؛ Cao، Yuan؛ Yong، Hai-Lin؛ Ren، Ji-Gang؛ Liang، Hao؛ Liao، Sheng-Kai؛ Zhou، Fei؛ Liu، Chang؛ Wu، Yu-Ping؛ Pan، Ge-Sheng؛ Zhang، Qiang؛ Peng، Cheng-Zhi؛ Pan، Jian-Wei (2007). "Classical statistical distributions can violate Bell-type inequalities". Journal of Physics A: Mathematical and Theoretical. ج. 41 ع. 8: 085303. arXiv:quant-ph/0703251. DOI:10.1088/1751-8113/41/8/085303.
- ^ Yin، Juan؛ Cao، Yuan؛ Yong، Hai-Lin؛ Ren، Ji-Gang؛ Liang، Hao؛ Liao، Sheng-Kai؛ Zhou، Fei؛ Liu، Chang؛ Wu، Yu-Ping؛ Pan، Ge-Sheng؛ Zhang، Qiang؛ Peng، Cheng-Zhi؛ Pan، Jian-Wei (2017). "After Bell". Fortschritte der Physik (Progress in Physics). ج. 65 ع. 1600014: 6–8. arXiv:1603.08674. Bibcode:2016arXiv160308674K.
- ^ Khrennikov، Andrei (2016). "After Bell". Fortschritte der Physik. ج. 65 ع. 6–8: 1600044. DOI:10.1002/prop.201600044.