مدار حدوة حصان
مدار حدوة حصان في علم الفلك (بالإنجليزية: Horseshoe orbit) هو نوع خاص من المدارات لجرم سماوي يتبع مدار جرم سماوي آخر (الأرض)، حيث يدور الاثنان حول جرم سماوي كبير مثل الشمس. من وجهة نظر إطار مرجعي ساكن يبدو مدار الجرم حول الشمس في هيئة قطع ناقص. ولكن بمشاهدة هذا الجرم السماوي من الأرض (إطار مرجعي متحرك) فتبدو لنا الحركة النسبية للجرم السماوي. ويظهر مدار الجرم السماوي في هذه الحالة في شكل قوس كبير لذهاب وإياب الجرم في السماء، ويشابه مداره عندئذ شكل حدوة الحصان.



أمثلة
عدل1) كويكب 2002 إيه إيه 29 الذي يتوافق مداره مع مدار الأرض حول الشمس، ويبلغ دورته حول الشمس سنة فلكية. يبدو مداره من الأرض في هيئة حدوة حصان.
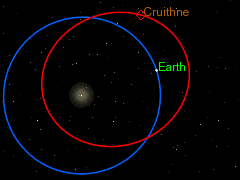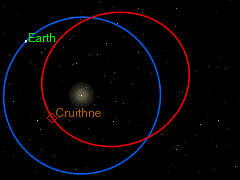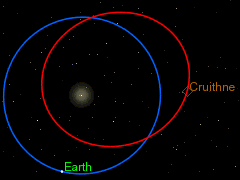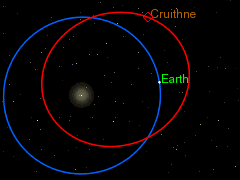
2) كويكب كرويثن 3753 ويتوافق مداره مع مدار الأرض حول الشمس. وتبلغ دورته حول الشمس 364 يوم. يبعد هذا الكويكب عنا عند أقرب نقطة نحو 13 مليون كيلومتر. يبدو مدار هذا الكويكب أيضا لنا على الأرض في شكل حدوة حصان (أنظر الشكل).
استقرار المدار
عدلنظرا لتقارب مدار الجرم السماوي لمدار الأرض حول الشمس، وكلاهما يدور حول الشمس، فتكون دورتيهما متقاربتين (365 يوم). فكل منهما واقع تحت تأثير جاذبية الشمس. ونظرا لتساوي دورتيهما الزمنية حول الشمس، فيقال أن لهما «رنين مداري» 1:1 . تلك المدارات تكون مستقرة إذا توفرت لها شروط، من أهمها أن يكون الجرم الثاني (الأرض) له كتلة أقل كثيرا من كتلة الشمس، فتغلب جاذبية الشمس المؤثرة على الكويكب، ويقل تأثير جاذبية الأرض عليه. كذلك يكون التأثير الأغلب على الأرض هو جاذبية الشمس بسبب كتلتها العظيمة، فتدور الأرض حول الشمس، ويكون تأثير جاذبية أي كوكب صغير مثل المريخ مثلا تأثيرا ضعيفا، وكذلك بالنسبة لأي كويكب فيكون تأثير جاذبيته على الأرض تأثيرا ضعيفا جدا.
و يلزم أن تكون كتلة الجرم السماوي (الكويكب) غير صغيرة جدا بحيث يستقر مداره.
التفسير
عدليبين الشكل 5 شكل مدار حدوة حصان لكوكب أو كويكب في المجموعة الشمسية: تدور الأرض ويدور الكويكب في عكس اتجاه الساعة حول الشمس. وتتغير المسافة بين الكويكب والأرض فهي تزداد في وقت وتقل في وقد آخر. تلك المواضع النسبية بين الكويكب وبين الأرض والشمس تتغير مع الزمن ويصبح شكلها شكل حدوة الحصان. يتشكل مدار حدوة الحصان كمحصلة لدورات تستمر 95 سنة، كما نرى في حالة كويكب 2002 إيه إيه 29 .
إذا افترضنا أن الكويكب موجود بالقرب من الأرض عند النقطة E في مدار دائري، غنظرا لوجود هذا المدار داخل مدار الأرض بالنسبة للشمس فتكون سرعته أسرع قليلا عن سرعة الأرض حول الشمس. ,[1] ويتحرك بطيئا مبتعدا عن الأرض. ويبقى الكويكب في هذا المدار حتى يكاد اتمام دورته حول الشمس.
وعندما يكون الكويكب قريبا من الأرض عند النقطة A - وهو الآن يكون خلفها ويلاحقها - فيتأثر الكويكب أيضا بجاذبية الأرض مما يزيد من سرعته على مداره. وبسبب زيادة قوة الطرد المركزية له (بسبب زيادة سرعته في مداره) فإنه ينزاح إلى الخارج وتزيد المسافة بينه وبين الشمس فتقل سرعته عن سرعة الأرض في مدارها (ابتداء من النقطة B) ولا يستطيع ملاحقتها ثم يدخل مداره ليصبح داخل مدار الأرض ثانيا.
وبعد فترة يبتعد الكويكب عن الأرض وتقل جاذبيتها له فلا يعاني من تسريع ويستمر في مداره الدائري حول الشمس ويبدو للأرض مبتعدا عنها (النقطة C). وهكذا تمر عشرات السنين يدور الكويكب في مداره حول الشمس - ولكنه يبدو للأرض كما لو يبتعد عنها.
بعد عشرات السنين يصبح الكويكب بالنسبة للأرض عن النقطة D وهنا أيضا يصبح تاثير جاذبية الأرض عليه كبير نسبيا ولكن في هذا الحالة من الجهة الأخرى، فيرتفع الكويكب في مداره وتنخفض سرعته، بالتالي ينخفض إلى مداره الدائري ويصبح داخل مدار الأرض. عندئذ تزيد سرعته حول الشمس ويبتعد عن تأثير جاذبية الأرض عليه. وهنا عند النقطة E يبدو سابقا الأرض من جديد.
يكتمل تشكل مدار حدوة الحصان لـ نيزك 2003 إبسيلون إن 107 بعد نحو 95 سنة.
انظر أيضًا
عدلالمراجع
عدل- ^ Dieser Zusammenhang ergibt sich aus der Formel für die Erste kosmische Kreisgeschwindigkeit. Das ist diejenige Geschwindigkeit, bei der sich Fliehkraft und Gravitationskraft aufheben. Es gilt dann d. h., ein Objekt in einem Orbit mit niedrigerem Radius hat eine größere Geschwindigkeit.