مؤشرات ميلر البلورية

مؤشرات ميلر البلورية (Miller index) في علم البلورات وعلم المعادن قيم تستخدم لتعريف المستويات والاتجاهات في أنظمة البلورات.^[1] وقد ابتكرت تلك الطريقة لوصف المستويات والاتجاهات في البلورة من العالم وليام ميلر عام 1839.

لتلك الطريقة استخدامات في علم البلورات من أجل التعريف بالمستويات المختلفة التي تتوزع فيها الذرات أو الأيونات في البلورة. كما تستخدم تلك المؤشرات في البحوث المتعلقة بتعيين البناء البلوري للمعادن والأملاح بواسطة حيود الأشعة السينية وحيود الإلكترونات وحيود النيوترونات. فخلال حيود الأشعة السينية مثلا، تنعكس أشعة إكس على مجموعة من المستويات المتوازية في البلورة مثلما تنعكس أشعة الضوء على المرآة، ويمكن بمعرفة طول موجة أشعة إكس الساقطة على البلورة معرفة زاوية انكسارها وقياسها. يمكن بواسطة تلك القياسات التعرف على النظام البلوري للمعدن، وإذا كنا نقوم بدراسة أحد المركبات أو الأملاح تعطينا شدة قياس الأشعة المنعكسة من البلورة مواضع توزيع الذرات المختلفة أو الأيونات في البناء البلوري.

كما يمكن بدراسة المتجهات في البناء البلوري في علم المواد معرفة أماكن الخلل في البناء البلوري أو التعرف على الشوائب الموجودة في البلورة.

تعريف المستويات

أمثلة لتعيين مؤشرات ميلر :إلى اليسار (111) وإلى اليمين (221).

يناء على أطوال الأضلاع الثلاثة لوحدة الخلية $\mathbf {a} _{1}$ و $\mathbf {a} _{2}$ و $\mathbf {a} _{3}$ . وعن طريق اختيار الثلاثة مؤشرات ميلر $\ell ,m,n$ وهي أعداد صحيحة أو مضاعفات لأعداد صحيحة.

نجد أن :

L يقطع المحور x عند a1
m تقطع المحور y عند a2
n تقطع المحور z عند a3

بذلك يكون المستوي البلوري المار بتلك الثلاث نقاط هو المستوي (111)

الحالة الثانية (221) نجد أن :

L يقطع المحور x عند a1/2
m تقطع المحور y عند 2/a2
n تقطع المحور z عند a3

ونظرا للاصطلاح على أن تكون مؤشرات ميلر دائما أعدادا صحيحة ، ينتج أن مؤشرات المستوي الجديد هي (221).

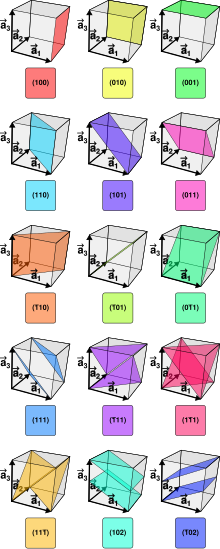
أمثلة للمستويات في النظام المكعب

نظام بلوري مكعب: بعض المستويات البلورية. يتصف كل مكعب بثلاثة محاور س ، ص ، ع ، تبدأ في الزاوية السفلى اليسارية الأمامية.

يبين الشكل عدة مستويات معرّفة بمؤشرات ميلر للنظام االبلوري المكعب ، ويمكن استنتاجها بنفس الطريقة المتبعة أعلاه مع نظام أحادي الميل.

مستويات بلورية

تكون الثلاثة أعداد صحيحة $h\!\,$ , $k\!\,$ und $l\!\,$ أعدادا ثلاثية $(hkl)\!\,$ وهذه هي مؤشرات ميلر. ويمكن لبعض الأعداد أن تكون سالبة (بحسب اتجاه اختيارنا لتلك الأعداد على المحاور الثلاثة z , y , x) فتميز هذه بشرطة فوق العدد ، مثل $({\bar {1}}0{\bar {2}})\!\,$ . وتعرف هذه الثلاثة مؤشرات أيضا مستوى معينا في البلورة.

وتوجد في البلورة عادة مجموعة من المستويات متكافئة ولا تختلف عن بعضها البعض ، فتعرف تلك الحالة بواسطة $\{hkl\}\!\,$ . مثال على ذلك نجد في نظام المكعب $\{100\}\!\,$ على أساس التناظر مجموعة المستويات المتكافئة $(100)\!\,$ , $({\bar {1}}00)\!\,$ , $(010)\!\,$ , $(0{\bar {1}}0)\!\,$ , $(001)\!\,$ و $(00{\bar {1}})\!\,$ , وهذه ماهي إلا الستة أوجة للمكعب ، وهي متكافئة.