قنطرة ويتستون
قنطرة ويتستون هي قنطرة كهربية لقياس المقاومات، اخترعها الإنجليزي صمويل كريستي عام 1833 وحسنها وأكملها شارلز وهيتستون عام 1843 .[1] وتـُجري عملية قياس المقاومة الكهربية المجهولة بعد تركيبها في دائرة كهربائية ذات فرعين (قنطرة) ثم موازنة التيار فيهما. وهي تعمل مثلما يعمل مقياس الجهد potentiometer ، مع الفرق أن في دائرة مقياس الجهد يستعمل جلفانومتر حساس.
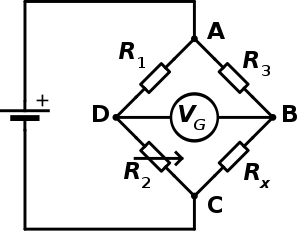
طريقة القياس
عدلفي الشكل المجاور تمثل المقاومة الكهربية Rx المقاومة المجهولة والمطلوب تعيينها .المقاومات و و معروفين ، في حين أن المقاومة قابلة للتغيير . فإذا تساوت نسبة المقاومتين الموجودتين في الفرع المعروف مع نسبة المقاومتين في الفرع الغير معروف يصبح فرق الجهد بين النقطتين B و D صفرا ولا يمر تيار كهربائي في الجلفانومتر . لذلك نغير المقاومة المتغيرة حتي نحصل على حالة الاتزان . وتوضح قراءة الجلفانومتر عما إذا كانت المقاومة كبيرة أم صغيرة.
ويمكن قراءة الجلفانومتر بدقة عالية . فإذا كانت المقاومات و و معروفة بدقة عالية ، أصبح من الممكن تعيين المقاومة المجهولة أيضا بدقة عالية.
عند الوصول إلى حالة التوازن ، تنطبق المعادلة :
وبناء على ذلك يكون:
وهناك حالة تكون فيها قيم المقاومات و و معروفة من دون أن تكون المقاومة قابلة للتغيير . في هذه الحالة نستطيع أن نستعمل قراءة فرق الجهد على مقياس الجهد أو شدة التيار المار فيه لتعيين المقاومة باستخدام قانون كيرشوف .
استنباط معادلة قنطرة وهيتستون
عدلنستخدم القاعدة الأولى من قانون كيرشوف للجهد للحصول على شدة التيار في النقطتين B و D:
ثم نستخدم القاعدة الثانية لقانون كيرشوف للحصول على فرق الجهد في جزئي الدائرة ABD و BCD:
نوازن القنطرة بحيث يكون ، بذلك يمكننا صياغة المعادلتين الأخيرتين بالطريقة الآتية :
بقسمة المعادلتين على بعضهما وعزل Rx على الجانب الأيسر ، نحصل على الصيغة التالية :
نعرف من القاعدة الأولى لكيرشوف أن و ، ويمكن حساب المقاومة المجهولة بواسطة المعادلة:
أصبحت الآن قيم الأربعة مقاومات معروفة وكذلك جهد المصدر . ويمكن تعيين فرق الجهد عبر القنطرة عن طريق تعيين جهد عند النقطتين B و D وطرح قيمتيهما . فتنطبق المعادلة :
ويمكن تبسيط تلك المعادلة لتصبح:
مراجع
عدل- ^ video نسخة محفوظة 7 سبتمبر 2019 على موقع واي باك مشين.