قانون حفظ الكتلة

ينص قانون حفظ المادة أو قانون حفظ الكتلة أو قانون بقاء المادة أو يعرف باسم قانون (لافوازييه-لومونوسوف) على ما يلي: عند حدوث أي تفاعل كيميائي فإن كتل المواد المتفاعلة تساوي كتل المواد الناتجة عن التفاعل، وأي كتلة في نظام مغلق تبقى ثابتة مهما حدث داخل النظام.

تفاعل الاحتراق من الميثان. حيث توجد 4 ذرات هيدروجين و4 ذرات أكسجين و1 ذرة كربون قبل التفاعل وبعده. الكتلة الكلية بعد التفاعل هي نفسها التي كانت قبل التفاعل.

يشير القانون إلى أن الكتلة لا يمكن خلقها أو تدميرها، على الرغم من إمكانية إعادة ترتيبها، أو تغيير شكل الكيانات المرتبطة بها. على سبيل المثال، في التفاعلات الكيميائية، كتلة المكونات الكيميائية قبل التفاعل تساوي كتلة المكونات بعد التفاعل. وبالتالي، أثناء أي تفاعل كيميائي وعمليات ديناميكية حرارية منخفضة الطاقة في نظام معزول، يجب أن تكون الكتلة الإجمالية للمواد المتفاعلة، أو المواد الأولية، مساوية لكتلة النواتج.

نظراً للجدل الدائم حول مصطلحي الكتلة والمادة فإن قانون بقاء الكتلة يبقى صحيحاً فقط للتقريب في الفيزياء الكلاسيكية بينما لا يمكن الاعتماد عليه في النسبية وفيزياء الكم في حين يظل قانونا بقاء الطاقة والزخم صحيحين.

يُستخدم مفهوم حفظ الكتلة على نطاق واسع في العديد من المجالات مثل الكيمياء والميكانيكا وديناميكا الموائع. تاريخيًا، أثبت ميخائيل لومونوسوف قانون حفظ الكتلة في التفاعلات الكيميائية بشكل مستقل ثم أعاد أنطوان لافوازييه اكتشافه لاحقًا في أواخر القرن الثامن عشر. كان لصياغة هذا القانون أهمية حاسمة في تقدم الخيمياء والعلوم الكيميائية الطبيعية الحديثة.

يُعتبر قانون حفظ الكتلة صحيحًا بشكل تقريبي وهو جزء من سلسلة من افتراضات نابعة من الميكانيكا الكلاسيكية. يجب تعديل القانون ليتوافق مع قوانين ميكانيكا الكم والنسبية الخاصة بموجب مبدأ تكافؤ الكتلة والطاقة، الذي ينص على أن الطاقة والكتلة تشكلان كمية واحدة محفوظة. بالنسبة للأنظمة ذات الطاقة العالية للغاية، لا ينطبق قانون حفظ الكتلة لوحده، كما هو الحال في التفاعلات النووية وإفناء الجسيمات للجسيمات المضادة في فيزياء الجسيمات.

بالإضافة لذلك، الكتلة غير محفوظة بشكل عام في الأنظمة المفتوحة. كما هو الحال عند السماح بخروج أو دخول أشكال مختلفة من المادة والطاقة من أو إلى النظام. مع ذلك، ما لم يكن هناك نشاط إشعاعي أو تفاعلات نووية، تكون كمية الطاقة التي تخرج (أو تدخل) من هذه الأنظمة، مثل الحرارة أو الشغل الميكانيكي أو الإشعاع الكهرومغناطيسي، صغيرة جدًا إذ لا يمكن قياسها على أنها انخفاض (أو زيادة) في كتلة النظام.

بالنسبة للأنظمة المُحاطة بحقول جاذبية كبيرة، يجب أن تُؤخذ النسبية العامة بعين الاعتبار، إذ يصبح حفظ الطاقة والكتلة مفهومًا أكثر تعقيدًا، يخضع لتعريفات مختلفة، ولا ينطبق حفظ الكتلة أو الطاقة بشكل صارم وبسيط كما هو الحال في النسبية الخاصة.

صياغة القانون وأمثله عليه

لا يمكن صياغة قانون حفظ الكتلة في الميكانيكا الكلاسيكية إلا عندما تكون مقاييس الطاقة المرتبطة بنظام معزول أقل بكثير من mc2، حيث (أمّ m) هي كتلة الجسم النموذجي في النظام، مُقاسة في الإطار المرجعي حيث يكون الجسم ساكنًا، و (سي c) هي سرعة الضوء.

يمكن صياغة القانون رياضيًا في مجالي ميكانيكا الموائع وميكانيكا الأوساط المتصلة، إذ يعبر عن حفظ الكتلة عادةً باستخدام معادلة الاستمرارية، بشكلها التفاضلي كما يلي:

• ${\frac {\partial \rho }{\partial t}}+\nabla \cdot (\rho \mathbf {v} )=0,$

حيث (رو ρ) هي الكثافة (الكتلة لكل وحدة حجم)، وt هو الزمن، و.∇ هو مؤثر التباعد، و (في v) هي سرعة التدفق. فيما يلي تفسير معادلة الاستمرارية للكتلة: بالنسبة لسطح مغلق معين في النظام، فإن التغير في الكتلة بالنسبة للزمن المُحاطة بالسطح يساوي مقدار الكتلة التي تعبر السطح، ويكون التغير موجبًا عند دخول المادة وسالبًا عند خروجها. بالنسبة لنظام معزول بالكامل، فإن هذا الشرط يعني أن الكتلة الكلية (أم M)، أي مجموع كتل جميع مكونات النظام، لا تتغير مع الزمن، وهو ما يُعبر عنه بالمعادلة الرياضية التالية:

${\frac {{\text{d}}M}{{\text{d}}t}}={\frac {\text{d}}{{\text{d}}t}}\int \rho {\text{d}}V=0$

حيث dV هو التفاضل الذي يعرف التكامل على كامل حجم النظام.

معادلة الاستمرارية للكتلة هي جزء من معادلات أويلر في ديناميكا الموائع. تصف العديد من معادلات الحمل الحراري والانتشار الأخرى حفظ وتدفق الكتلة والمادة في نظام معين.

في الكيمياء، يجري حساب كمية المواد المتفاعلة والناتجة في التفاعل الكيميائي، وهو ما يُعرف باسم قياس اتحادية العناصر، بالاعتماد على مبدأ حفظ الكتلة. ينص المبدأ على أنه خلال التفاعل الكيميائي، تكون الكتلة الكلية للمواد المتفاعلة مساوية للكتلة الكلية للمواد الناتجة. على سبيل المثال، في التفاعل التالي:

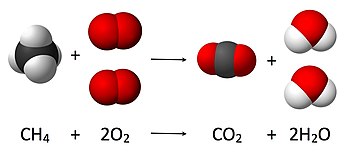
CH4 + 2O2 → CO2 + 2H2O

يتحول جزيء واحد من الميثان (CH4) وجزيئين من الأكسجين ((O2 إلى جزيء واحد من ثاني أكسيد الكربون (CO2) وجزيئين من الماء (H2O). يمكن اشتقاق عدد الجزيئات الناتجة عن التفاعل من مبدأ حفظ الكتلة، إذ يوجد في الحالة الابتدائية أربع ذرات هيدروجين وأربع ذرات أكسجين وذرة كربون واحدة (وكذلك في الحالة النهائية)، بالتالي فعدد جزيئات الماء الناتجة يجب أن يساوي اثنين لكل جزيء ثاني أكسيد الكربون ناتج.

تُحل العديد من المسائل الهندسية باتباع التوزيع الزمني للكتلة لنظام معين، تُعرف هذه الطريقة باسم توازن الكتلة.

نظرة تاريخية

كانت الفكرة المهمة في الفلسفة اليونانية القديمة هي أن «لا شيء يأتي من العدم،» فما هو موجود الآن كان موجودًا دائمًا: لا يمكن أن تُخلق مادة جديدة من لا شيء. هناك بيان صريح لهذا المبدأ، إلى جانب المبدأ الإضافي القائل بأن لا شيء يمكن أن يفنى إلى العدم، في مقولة أمبادوقليس (نحو القرن الرابع قبل الميلاد): «من المستحيل أن يأتي أي شيء من لا شيء، ولا يمكن إحداث أو سماع ما هو معدوم تمامًا.»

ذكر إبيقور مبدًأ آخر للحفظ في نحو القرن الثالث قبل الميلاد، وصف فيه طبيعة الكون، إذ ينص على أن «مجموع الأشياء كان دائمًا كما هو الآن، وسيستمر ذلك للأبد.»

تنص فلسفة جاينية، وهي فلسفة لا خلقية، تستند على تعاليم ماهافيرا (القرن السادس قبل الميلاد)، على أنه لا يمكن تدمير أو خلق الكون ومكوناته مثل المادة. تنص المخطوطة الجاينية تاتفارثاسوترا (القرن الثاني بعد الميلاد) على أن المادة دائمة، ولكن تختلف أشكالها من خلال الخلق والفناء. ونص مبدأ نصير الدين الطوسي (نحو القرن الثالث عشر الميلادي) على مبدأ حفظ المادة. إذ كتب أنه «لا يمكن للجسم المادي أن يختفي تمامًا. فهو يغير فقط شكله وحالته وتكوينه ولونه وخصائصه الأخرى ويتحول إلى مادة مختلفة معقدة أو بسيطة.»

الاكتشافات في الكيمياء

بحلول القرن الثامن عشر، كان مبدأ حفظ الكتلة أثناء التفاعلات الكيميائية مستخدمًا على نطاق واسع وكان افتراضًا مهمًا خلال التجارب، حتى قبل تعريفه بشكل رسمي، كما هو واضح في أعمال جوزيف بلاك وهنري كافينديش وجين راي. كان أول من حدد هذا المبدأ هو ميخائيل لومونوسوف في عام 1756. إذ برهنه من خلال عدة تجارب وناقشه من قبل في عام 1774 في مراسلاته مع ليونهارت أويلر، على الرغم من معارضة ادعاءاته حول هذا الموضوع في بعض الأحيان. أجرى أنطوان لافوازييه في وقت لاحق سلسلة أكثر دقة من التجارب، إذ عبر عن استنتاجه في عام 1773 وجعل مبدأ حفظ الكتلة مشهورًا. استبدلت براهين هذا المبدأ النظريات التي عفا عليها الزمن، مثل نظرية فلوجستون التي زعمت أنه يمكن كسب الكتلة أو فقدها في عمليات الاحتراق والحرارة.

كان حفظ الكتلة مبدًأ غامضًا منذ آلاف السنين بسبب تأثير الطفو في غلاف الأرض الجوي على وزن الغازات. على سبيل المثال، تزن قطعة الخشب أقل بعد احتراقها؛ بدا أن هذا يشير إلى اختفاء بعض كتلتها أو تحولها أو فقدانها. لم يجر دحض هذا الادعاء حتى أُجريت تجارب دقيقة سمحت بحدوث تفاعلات كيميائية مثل الصدأ في أمبولات زجاجية مُحكمة الغلق؛ إذ تبين أن التفاعل الكيميائي لم يغير من وزن الحاضنة المغلقة ومحتوياتها. لم يكن من الممكن قياس وزن الغازات باستخدام الموازين حتى اختراع المضخة الفراغية في القرن السابع عشر.

التاريخ

أول من أشار لقانون حفظ الكتلة هو العالم المسلم الأندلسي أبو القاسم مسلمة بن أحمد المجريطي، وذلك في كتابه «رتبة الحكيم».

انظر أيضًا

• بقاء الطاقة
• حفظ الزخم