طول (جغرافيا)
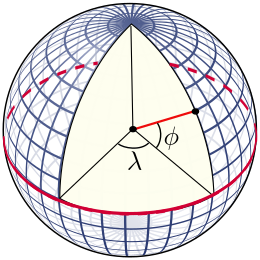
في الجغرافيا، الطُول[1][2] أو الطول الجغرافي هو إحداثي يحدد موقع نقطة على سطح الأرض شرقًا أو غربًا؛ بتعبير آخر، خط الطول هو قياس زاوية بين شاقول المكان ومستوى خط غرينيتش، يُعبَّر عنه عادةً بالدرجات ويُشار إليه بالحرف اليوناني لامدا (λ). خطوط الطول هي أنصاف دوائر عظمى وهمية توصل بين القطب الشمالي والقطب الجنوبي وتربط نقاط متساوية خط الطول، ويبلغ عددها 360 خط، ويبدأ العد من الخط الصفري المار بغرينيتش. خط غرينيتش هو خط الطول 0 وهو يمر بمدينة غرينيتش في بريطانيا. بين كل خطين متتاليين 1°. وبالتحرك شرقا يأتي خط الطول 1°، ثم خط الطول 2 ° وهو الحدود الشرقية لـ المملكة المتحدة، كما نجد باريس على خط طول 2°(درجة)، و 21' (دقيقة (زاوية)، وهكذا نجد الإسكندرية على خط طول 30° شرقا. بالمثل عند التحرك في اتجاه الغرب من غرينتش يعد خط الطول 1° ولكن غربا، ثم 2 ° غربا، وهكذا. يُستخدم العرض والطول معًا إحداثيينٍ لتحديد موقع على سطح الأرض.
| صنف فرعي من | |
|---|---|
| جزء من | |
| رمز الكمية | |
| البعد حسب النظام الدولي للكميات | |
| النقيض |

نعطي هنا بعض المدن الشهيرة وطولها الجغرافي:
- غرينيتش = 0°
- غرب باريس = 2° شرقا
- مدينة تونس = 10° شرقا
- القدس = 35° شرقا
- موسكو = 37° شرقا
- مكة المكرمة = 40° شرقا
- كابل = 69° شرقا
- جاكرتا = 106 ° شرقا
- هونغ كونغ = 114 ° شرقا
- طوكيو = 121 ° شرقا
- هاواي = 155 ° غربا
- سان فرانسيسكو = 122 ° غربا
- نيويورك = 73 ° غربا
- إيرلندا = 8 ° غربا
نلاحظ أن عدد خطوط الطول شرقا 180 وعدد خطوط الطول غربا 180، والجميع يكملون دائرة زاويتها 360 °. هذا التقسيم اتفقت عليه جميع الدول.
بهذا النظام يحدد التوقيت في مختلف دول العالم، لأن الكرة الأرضية تدور حول محورها من الغرب إلى الشرق. بل أن هذا النظام يحدد أيضا توقيت المدن المختلفة؛ فالمسلمون مثلا يؤدون صلواتهم حسب توقيت مدينتهم أو قريتهم المحلية. لهذا ليس غريبا أن يشمل تقسيم الطول بالدرجة الزاوية، والدقيقة الزاوية، والثانية الزاوية؛ فكل درجة من الطول مقسمة إلى 60 دقيقة، وكل دقيقة مقسمة إلى 60 ثانية. الطول 80 يكون درجته 80°، وموقع المدينة المنورة مثلا نجده على طول = 39.6 شرق، أو بتعبيرٍ آخر، 39° 36' 0" شرق.
ولكن الطول الجغرافي للمدينة المنورة هذا يتفق مع خط الطول الذي تقع عليه مدينة الرقة في سوريا. لهذا لا بد من إدخال العرض في الاعتبار للتعريف بالبلد، فنجد إحداثيات المدينة المنورة هي :
- الطول = 39.6
شرقا
- العرض = 24.46667
شمالا
وأما الرقة فإحداثياتها:
- الطول = 39.01667
شرقا
- العرض = 35.95
شمالا
الدراسة والاكتشاف
عدل- في 1612م اقترح غاليليو غاليلي أن بالمعرفة الدقيقة لمدارات أقمار المشتري يمكن استخدام مواقعها كساعة عالمية، وأن هذا سيساعد على إمكانية تحديد خطوط الطول على الأرض بدقة. ولكن الإسلوب الذي وضعه غاليليو لم يكن عمليا للملاّحين على متن السفن البحرية.
- وفي عام 1714م أصدرت الحكومة البريطانية «قانون الطول الجغرافي»، حيث عرضت مكافآت مالية كبيرة للشخص الأول الذي يستطيع وضع طريقة عملية لتحديد الطول الجغرافي من داخل السفن البحرية، لحل مشاكل البحارة في تحديد مواقعهم في البحار.
- بمقارنة موقع كل من القمر والمريخ مع مواقعها المتوقعة، كان فسبوتشي قادرا على تحديد الطول. ولكن هذا الإسلوب واجه عدّة قيود:
- أولاً، أنه يتطلّب حدوث حدث فلكي معين (اصطفاف القمر والمريخ على نفس السوية بالنسبة للأرض)، وهذا يتطلّب المراقبة المستمرة لاستباق هذا الحدث عن طريق وضع تقويم فلكي.
- ثانيا، يجب معرفة الوقت بشكل دقيق، حيث كان من الصعب التأكد من أراض أجنبية.
- وأخيراً، هذه الطريقة تتطلب منصة قياس مستقرة، مما يجعل هذه التقنية عديمة الفائدة على متن سفينة بحرية تهتز.
- اخترع الإنكليزي جون هاريسون، (الكرونومتر البحري)، وهي أداة رئيسية لحل مشكلة الدقة في تحديد الطول في البحر، وبهذه الطريقة زادت إمكانية البحارة في قطع مسافات طويلة في البحار[3]، وعلى الرغم من أن جون هريسون حصل على المكافأة التي وضعتها الحكومة البريطانية لاختراعه (الكرونومتر البحري) سنة 1773، إلا أن الكرونومتر ظل مكلفا للغاية وإسلوب المسافة القمرية ظل هو الإسلوب المستخدم لعدّة عقود.
- وأخيراً، تم تنسيق عمل الكرونومترات البحرية وإشارات التلغراف اللاسلكي، الأمر الذي وضع حلا نهائيا لمشكلة تعيين الطول في القرن العشرين.
أهمية خطوط الطول
عدلتُفيد في تحديد الزمن و فروق التوقيت بين المدن، أيضا تسهل دراسة الكرة الأرضية.
قياس خطوط الطول مهم على حد سواء لرسم الخرائط والمحيطات وللملاحة أيضا. معظم المستكشفين عانوا على مر التاريخ من مشكلة تحديد خطوط الطول، حيث استغرق العثور على وسيلة لتحديد خطوط الطول عدة قرون.
دوائر العرض
عدللتكملة الإحداثيات الجغرافية لتعيين مواقع المدن المختلفة ومواقع السفن في البحر، أُضيفت دوائر عرض إلى خطوط الطول . دوائر العرض هي دوائر وهمية على سطح الكرة الأرضية تبدأ بالخط 0 وهو خط الإستواء . وتقسم المناطق الشمالية بدوائر بين 0 درجة و 90 درجة وتسمّى شمالا؛ وتقسم المناطق الجنوبية على الأرض إلى دوائر بين 0 (خط الإستواء) و 90 جنوبا.
تم احتساب دوائر العرض من خلال مراقبة الرباعي أو أسطرلاب، و ارتفاع الشمس أو النجوم وتم رسمها بشكل دوائر أفقية على الخرائط.
بواسطة معرفة خط الطول ودائرة العرض التي تقع عليها مدينة ما، يمكن التعرف على المدينة (أنظر مثال المدينة المنورة والرقة أعلاه).
حساب خطوط الطول
عدلويعطى الطول الجغرافي كمقياس زاوي يتراوح بين 0° على خط الطول الرئيسي + 180 ° شرقا وغربا −180°. الحرف اليوناني λ (لامدا)، [4][5] يستخدم للدلالة على الموقع إذا كان شرق أو غرب خط الطول الرئيسي.
كل درجة من الطول شبه مقسمة إلى 60 دقيقة، وينقسم كل منها إلى 60 ثانية. ويتم كتابة طول بهذه الطريقة 30 23° 27′ هي المحدد الثواني مع كسر عشري. يستخدم تمثيل بديل درجة ودقيقة، حيث عن أجزاء لمدة دقيقة بالتدوين العشري مع جزء صغير، وبالتالي: كما يمكن التعبير عن 27.500′ 23° ككسر عشري: 23.45833 درجة شرقا لإجراء العمليات الحسابية، قد يتم تحويل قياس الزوايا بالتقدير الدائري، حتى أنه يمكن التعبير عن الطول الجغرافي بدلالة π، حيث كل واحد باي يساوي 180°. لإجراء العمليات الحسابية، يتم استبدال الشرق والغرب بعلامة سالبة في نصف الكرة الغربي وعلامة إيجابية في النصف الشرقي. حيث يمكن الجمع بين طول جغرافي محدد و عرض جغرافي محدد (عادة ما يكون العرض موجب في نصف الكرة الشمالي) تعطي موقعا دقيقا على سطح الأرض وهذا يتم باستخدام نظام الاحداثيات الديكارتي (جملة ديكارت) وقد يحدد الطول عند نقطة معينة بحساب الفارق الزمني بين الموقع المراد حساب الطول عنده و «التوقيت العالمي» (UTC). إن هناك 24 ساعة في يوم و 360 درجة في حلقة مفرغة، تتحرك الشمس بالنسبة للأرض بمعدل 15 درجة كل ساعة (360 درجة/24 ساعة = 15 درجة للساعة الواحدة). إذا كان هناك شخص ما في المنطقة الزمنية (UTC -3) ثلاث ساعات قبل التوقيت العالمي) فإن هذا الشخص موجود قرب خط طول 45° (3 ساعات × 15 ° كل ساعة = 45 °). واستخدمت الكلمة قرب نظراً لأن هذه النقطة قد لا تكون في وسط المنطقة الزمنية؛ كما يتم تعريف المناطق الزمنية سياسيا، حتى تلك المراكز والحدود، وهذا يؤدي في كثير من الأحيان ألّا تكون خطوط الطول من مضاعفات 15°. فهاذا يفرض وجود الكرونومتر لحساب الطول في موقع معين حيث يعين التوقيت العالمي المنسق UTC، وتحديد التوقيت المحلي عن طريق المراقبة الفلكية أو الطاقة الشمسية.
- وترد تفاصيل أكثر تعقيداً مما هو موضح هنا في المقالات التالية:
- مقالة عن التوقيت العالمي
- مقالة عن معادلة الوقت .
خواص خطوط الطول
عدلباستخدام خطوط الطول، استطاع العلماء حساب الزمن في مدينة معينة بمعرفة زمن مدينة أخرى، وكذلك خط طولها وذلك باستخدام الخواص التالية لخطوط الطول استطاعوا حساب:
- المدن التي على خط طول واحد لها نفس التوقيت تقريبا، فمثلا الساعة في مدينة القاهرة 5:00 ص وهي على خط طول 30° شرقا (شرق جرينتش) فإن الساعة ستكون في الخرطوم 5:00 ص، ويرجع ذلك أن خط الطول الذي يمر بالقاهرة هو نفس خط الطول الذي يمر بالخرطوم.
- عند دوران الأرض حول نفسها فإنها تأخذ 4 دقائق بين كل خط طول والآخر أي أن فرق الزمن بين كل خط طول والآخر 4 دقائق، وكذلك أيضا فإنها تشرق على 15 خط طول في الساعة.
- الأرض تدور من الغرب إلى الشرق حول نفسها. ويعني ذلك أن المدن التي تقع شرق خط جرينتش تشرق عليها الشمس قبل التي تقع غربه.
كيفية حساب فرق التوقيت
عدلمثال : إذا كانت الساعة في مدينة جرينتش الآن 7:30 مساء فكم تكون الساعة في مدينة القاهرة الواقعة على خط الطول 30° شرقا
اولا يحسب فرق الخطوط وهو طرح خطي الطول من بعضهما
الفرق بين خطي الطول = 30 – 0 = 30° خط طول
ثم يحسب فرق زمن دوران الأرض حول نفسها بين المدينتين بضرب خط طول القاهرة 30 في 4 ، حيث 4 هو فرق الزمن بين إشراق الشمس بين خطي متتاليين . (زاوية 1 ° تعادل 4 دقائق زمنية)
فرق الزمن بين القاهرة وغرينيتش = 30 × 4 = 120 دقيقة
فرق التوقيت بالساعات = = ساعتين
ثم يُضاف الزمن الموجود في مدينة غرينتش (المدينة المعروف توقيتها) إلى فرق الزمن إذا اتجهنا شرقا ؛ ويُطرح إذا اتجهنا غربا . وبما أن القاهرة في الشرق فإننا نضيف ساعتين على توقيت غرينيتش وبذلك نعرف توقيت القاهرة. الزمن في القاهرة = 2 + 7.30 = 9.30
إذاً الساعة في القاهرة 9:30 حسب «توقيت جرينتش».
المراجع
عدل- ^ إدوار غالب (1988). الموسوعة في علوم الطبيعة: تبحث في الزراعة والنبات والحيوان والجيولوجيا (بالعربية واللاتينية والألمانية والفرنسية والإنجليزية) (ط. 2). بيروت: دار المشرق. ج. 2. ص. 1008. ISBN:978-2-7214-2148-7. OCLC:44585590. OL:12529883M. QID:Q113297966.
- ^ لويس معلوف (1986)، المنجد في اللغة والأعلام (ط. 26)، بيروت: دار المشرق، ص. 472، OCLC:1184173733، QID:Q124029920
- ^ ا ب "Longitude clock comes alive". BBC. March 11, 2002. نسخة محفوظة 08 أكتوبر 2017 على موقع واي باك مشين.
- ^ Coordinate Conversion نسخة محفوظة 29 سبتمبر 2009 على موقع واي باك مشين. [وصلة مكسورة]
- ^ "λ = Longitude east of Greenwich (for longitude west of Greenwich, use a minus sign)."
John P. Snyder, Map Projections, A Working Manual, الماسح الجيولوجي الأمريكي Professional Paper 1395, page ix نسخة محفوظة 01 يوليو 2010 على موقع واي باك مشين.
انظر أيضاً
عدل- عرض جغرافي
- خط الطول
- دائرة العرض
- غرينتش
- خط الاستواء
- جغرافيا
- علوم الأرض
- علم تشكل الأرض
- سماء الربيع
- سماء الشتاء
- خارطة النجوم