تقييد كمومي
تقييد الكم (بالإنجليزية: Quantum confinement) يعني بصورة مبسطة حبس الإلكترون داخل صندوق أي إبقاءه ضمن حجم محدود وحصره بداخله، ويحدد طول هذا الصندوق وعرضه وارتفاعه خواص نقطة الكم (الإلكترون المقيد) والتي يعبر هنا «بئر جهدي» ومستويات طاقته وشكلها، ويعد الإلكترون المرتبط بالنواة الذرية واقعاً تحت تأثير جهدها الكهربائي فيكون كما لو كان مقيداً داخل صندوق، وأحياناً يكون هذا التشبيه بأن الإلكترون منحصر في «بئر كهربائي كولومي (بئر الكم)»، يتطلب الإلكترون امتلاك طاقة معينه تسمح له بالخروج من البئر (أنظر جسيم في صندوق).

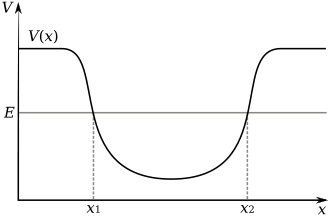
إذا كان الإلكترون موجوداً في صندوق كبير فإنه يتصرف كما لو كان حراً، فهو لا يقع تحت تأثير أي جهد، في تلك الحالة يمكن للإلكترون امتلاك طاقة بحيث تكون مستويات الطاقة له متداخلة مع بعضها البعض (متصلة وليست منفصلة) هذا هو تصرف الإلكترون أو الجسيم عندما يكون حجم الصندوق كبير ويضمحل تأثير حجم الإلكترونات فيه، إذن ما معيار كبر حجم الصندوق؟ ما هو طول التقييد الملائم؟ المعيار هنا هو تحدده خواص الإلكترون.
في عام 1924 اقترح لويس دي برولي أن الجسيمات دون الذرية مثل الإلكترون تكون مقترنة بموجة معتمدة على كتلته وسرعة الجسيم، جاءت تلك الفكرة من عدة ظواهر في الفيزياء يظهر فيها الإلكترون كأنه يتصرف كجسيم مثل تجربة الشق المزدوج وفي تجارب أخرى يتصرف كموجة مثل تجربة يونج، وتقول نظرية ازدواجية موجة-جسيم التي صاغها «دي برولي» أن الجسيم يكون مقترناً بموجة يتحدد طول موجتها بناءً على كتلة الجسيم وسرعته.

إذا كانت أبعاد الصندوق كبيرة مقارنة بطول موجة الإلكترون أو بمصطلح أدق أكبر كثيراً من نصف قطر بور (نصف قطر ذرة الهيدروجين) فإن الإلكترون لا يعد مقيداً. أما حين تكون أبعاده مساوية لطول الإلكترون الموجي فإن مستويات طاقة الإلكترون تظهر منفصلة descrit values(بمعنى أنها تتخذ قيم خاصة)، وبذلك تصبح فجوة النطاق محكومة بحجم الصندوق وموضع الإلكترون. .[1]
كان هذا مثال أولي فكر فيه الفيزيائيون خلال الثلاثين سنة الأولى من القرن العشرين كمحاولة لفهم تركيب الذرة بعد اكتشاف الإلكترون والبروتون، وعرفوا أن ذرة الهيدروجين هي أبسط الذرات حيث تتكون من بروتون واحد (يمثل نواة الذرة) ويدور حولها الإلكترون، وكان محيراً لهم طيف الهيدروجين الذي يظهر في هيئة خطوط طيفية منفصلة عن بعضها البعض وكل منها يتميز بتردده الخاص.
فكان نموذج التقييد في صندوق أحد النماذج المبسطة لحل المسألة، وبمرور الوقت طور العلماء نماذجهم للبنية الذرية بحيث استطاعوا بعد ذلك حل لغز تصرف الإلكترون في الذرة، وأن يصيغوا نظرياتهم في هيئة معادلات يحسبون بها ترددات الضوء التي يشعها الإلكترون في طيف الذرة، من تلك النماذج أيضا ما يسمى بئر الكم (بالإنجليزية: Quantum well).[2]
وبحلول عام 1925 استطاع الفيزيائي الألماني فرنر هايزنبرج الحصول على الصيغ الرياضية التي تفسر طيف الهيدروجين تماماً، وكانت طريقته تعتمد على استخدام المصفوفات ولهذا سميت نظريته ميكانيكا المصفوفات وهي تعتمد على التصور التكميمي للطاقة، والتي كان ماكس بلانك قد إقترحها عام 1900 محاولاً تفسير النتائج الغريبة للتجارب العملية عن إشعاع الجسم الأسود، ثم قدم إرفين شرودنغر عام 1926 وصاغ معادلته المسماة باسمه «معادلة شرودنجر» التي استفاد فيها من فروض دي برولي حول الخاصية الموجية للجسيمات ونجحت معادلته في تفسير الطيف ذرة الهيدروجين، لتصبح معادلته ذات أهمية كبرى في نظرية ميكانيكا الكم التي شارك في صياغتها علماء عظماء مثل ماكس بلانك ونيلز بور ولويس دي برولي وفولفجانج باولي وفيرنر هايزنبرج وماكس بورن وبول ديراك وآخرين، فقد نجحت نظرياتهم في تفسير ظواهر عديدة في الطبيعة مثل التوصيل الكهربائي العوازل وأشباه الموصلات، وكلها ظواهر نشأت منها اختراعات مثل الهاتف والتلفزيون وميكروبروسيسور والحاسوب وغيرها، التي أصبحت اليوم من الأشياء التي لا يمكن الإستغناء عنها.
المراجع
عدل- ^ Quantum Dots: Confinement and Applications. نسخة محفوظة 06 يوليو 2010 على موقع واي باك مشين.
- ^ What is a quantum well?. نسخة محفوظة 02 يوليو 2017 على موقع واي باك مشين.

