تحويل لورينتز

تحويل لورينتز (بالإنجليزية: Lorenz transformation)‏ عبارة عن مجموعة تحويلات تستخدم لتحويل الإحداثيات المكانية والزمانية (أو بشكل عام أي متجه رباعي الأبعاد) في إطار مرجعي عطالي س إلى الإحداثيات الأربعة في إطار مرجعي آخر ع. تعتمد تحويلات لورينتز على وجود سرعة قصوى في الكون لا يمكن للأجسام تعديتها، ألا وهي سرعة الضوء c في الفراغ.

تحويلات لورينتز

معلومات عامة

سُمِّي باسم	هندريك أنتون لورنتس
المكتشف أو المخترع	هندريك أنتون لورنتس
تعريف الصيغة	$t'=\gamma \left(t-{\frac {vx}{c^{2}}}\right),x'=\gamma \left(x-vt\right)$

إحداثي زمكان لحدث، كما يقاس عبر كل مراقب في إطار عطالي مرجعي

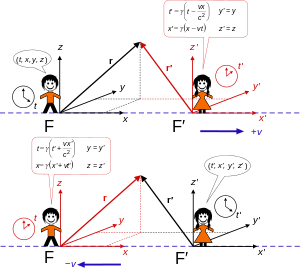
فاذا حصل الحدث في الإطار المرجعي العطالي (مختبر) س بالإحداثيات $(t,x,y,z)$ وشوهد الحدث نفسه من «المختبر» ع بالإحداثيات $(t',x',y',z')$ فيحتم مبدأ النسبية (تساوي القوانين الطبيعية في س وع) مع اعتبار سرعة الضوء c هي أقصي سرعة في الكون للأجسام ولانتقال الطاقة، فتوصل لورينتز إلى التحويلات الآتية:

$t'=\gamma \left(t-{\frac {vx}{c^{2}}}\right)$

$x'=\gamma (x-vt)\,$

$y'=y\,$

$z'=z\,$

حيث:

$x$ و$y$ و$z$ هي إحداثيات المكان،

$t$ إحداثي الزمن،

$v$ سرعة الجسم

$c$ سرعة الضوء في الفراغ.

و

$\gamma \equiv {\frac {1}{\sqrt {1-v^{2}/c^{2}}}}$ يدعى معامل لورينتز

كما توجد معادلات تحويل عكسية تسمى معادلات لورينتز العكسية.

تاريخ

فكر لورنتز في تلك التحويلات بعد أن أتت تجربة ميكلسون ومورلي عام 1881 بنتيجة غير متوقعة. فقد أجرى العالمان «ميكلسون» و«مورلي» تجربتهما الشهيرة لتعيين سرعة الضوء فيما كان يسمى «أثير»، اعتقد العلماء آنذاك بوجوده في الفراغ لتفسير انتقال الضوء فيه، مثلما ينتقل الصوت في وسط مثل الهواء أو الماء (لا ينتقل الصوت في الفراغ). وكانت تجربة ميكلسون ومورلي مبنية على فكرة تعيين سرعة الضوء في اتجاهين متعامدين أحدهما في اتجاه حركة الأرض في دورانها حول الشمس. وباعتبار أن الأرض تسبح في «أثير» بسرعة 30 كيلومتر في الثانية، فكان لا بد وأن تختلف سرعة الضوء في اتجاهين عكسيين أو في اتجاهين متعامدين. ولكن لم يظهر في التجربة أي اختلاف في سرعة الضوء، بمعنى أنه لا يوجد أثير ينتقل بواسطته الضوء. وكانت تلك النتيجة غير متوقعة وحيرت العلماء.

فكانت فكرة لورينتز للخروج من ذلك المأزق أنه ربما يحدث في تجربة ميكلسون تقلص في طول المسافة التي كان يقيسها ميكلسون ومورلي في تجربتهما، وأتت تحويلاته فعلا بتقلص لتلك المسافة متعلقا بالنسبة بين سرعة الأرض v في الفضاء وسرعة الضوء c. وفي عام 1905 صاغ ألبرت أينشتاين النظرية النسبية الخاصة -وكان عمره 25 سنة - وفسر مسألة انتشار الضوء على أساس أن الضوء هو أقصي سرعة في الكون وأنها ثابت فيزيائي في الفراغ لا تتغير. وتتضمن النظرية النسبية تحويلات لورينتز.

في حياتنا اليومية نتعامل مع سرعات بطيئة جدا بالنسبة لسرعة الضوء، وسرعة الضوء كبيرة جدا فهي تبلغ 300,000 كيلومتر في الثانية (أي يلف شعاع كهرومغناطيسي مثل الضوء حول الأرض سبع مرات في ثانية واحدة). لذلك لا نلاحظ الـتأثيرات النسبية (مثل تقلص الأطوال، إبطاء زمني، أو تراقص السرعات) عند تلك السرعات البطيئة، وتصلح في تلك المسائل استخدام تحويل جاليليو بين إطارين مرجعين (وهذا هو ما تعودناه). أما عندما تقترب سرعة الجسم من سرعة الضوء فلا بد من استخدام تحويلات لورينتز، فتحويلات جاليليو هي تقريبية بمقارنتها بتحويلات لورينتز، ولا يصح استخدام تحويل جاليليو في سرعات كبيرة.

تغير الكتلة مع زيادة السرعة

تعودنا على أن الكتلة لا تتغير بزيادة السرعة. ويعود ذلك إلى اننا نعتبر أن السرعة تتزايد بتزايد الزمن الذي تؤثر فيه قوة على الجسم باعتبار تلك القوة ثابتة. ويقوم هذا الاستنتاج على القانون المعتاد لتجميع السرعات. ولكن النظرية النسبية الخاصة تقول أنه يوجد حد أقصى للسرعات، أي اننا لا نستطيع في جميع الأحوال تطبيق قانون جمع السرعات المعتاد.

كيف نستطيع تعيين سرعة جسم بعد الثانية الثانية لتأثير القوة عليه؟ إننا نجمع السرعتين، السرعة التي اكتسبها خلال الثاتية الأولى مضافا إليها السرعة التي اكتسبها الجسم خلال الثانية الثانية وذلك طبقا لقانون جمع السرعات العادي بدقة لا بأس بها. ولكننا نستطيع إجراء ذلك إلى ان نقترب من سرعة الضوء. وفي تلك الحالة لا يصح استخدام القانون المعتاد من الميكانيكا الكلاسيكية. عندما نجمع السرعات طبقا للنطرية النسبية نجد انها تعطي سرعة أقل من السرعة التي يحسبها القانون العادي. وهذا معناه أن السرعات العالية لا تتناسب طرديا مع الزمن الذي تؤثر خلاله القوة على الجسم، وإنما يتم ذلك أبطأ بكثير. ويتضح لنا ذلك بمعرفة وجود حد أقصى للسرعات.

فعندما تقترب سرعة جسم تحت تاثير قوة من سرعة الضوء فانها تزداد أقل فأقل، بحيث لا تتعدى الحد الأقصى للسرعات. وطالما اعتبرنا أن سرعة الجسم تتناسب تناسبا طرديا مع زمن تأثير القوة على الجسم يحق لنا اعتبار أن الكتلة لا تعتمد السرعة. ولكن عندما تقترب سرعة الجسم من سرعة الضوء في الفراغ فلا يصبح هذا التناسب بين الزمن والسرعة قائما، وتصبح الكتلة معتمدة على السرعة. ونظرا لأن زمن التسريع يمكن أن يطول إلى مالانهاية بينما لن تتعدى سرعة الجسم الحد الاقصي للسرعة، فنستنتج من ذلك أن الكتلة تزداد بزيادة السرعة، وتتخذ قيمة لا نهاية عندما تصل سرعة الجسم سرعة الضوء.

وتبين الحسابات أن تغير كتلة الجسم بازدياد سرعته هو تغير ينم بنفس معدل تقلص طوله طبقا لمعادلة لورينتز. فإدا كان جسم يتحرك بسرعة 240,000 كيلومتر في الثانية تصل كتلته إلى 1.6 من كتلته في حالة السكون (سرعة الضوء في الفراغ تبلغ 300,000 كيلومتر في الثانية).

فكان من الطبيعي أنه عند تعاملنا مع سرعات اقل بكثير من سرعة اضوء أن نعتبر أن كتلته ثابتة لا تعتمد على السرعة، مثلما نعتبر ان طوله لا يعتمد على سرعته. وقد اختبرت زيادة كتلة الإلكترون مع زيادة سرعته عمليا وثبتت تلك الحقيقة. فقد أصبح معتادا تسريع الالكترونات والأنوية المشحونة إلى سرعات قريبة من سرعة الضوء. ووصلنا إلى تسريعها في بعض معجلات الجسيمات إلى سرعة 99.9999 % من سرعة الضوء أي أقل من سرعة الضوء فقط بمقدار 300 متر/ثانية. ويمكن للفيزيائيين مقارنة كتلة الإلكترون الساكن بكتلة الإلكترون السريع. وتتفق نتائج التجارب على أن الكتلة تزداد بزيادة سرعة الجسم طبقا لمعادلات لورينز، ويتفق ذلك تماما مع مبدأ النسبية.

طبقاً لقانون الكتلة النسبية فإن الجسم الذي تزيد سرعته إلى أن تساوى سرعة الضوء سوف تكون كتلته لا نهائية، وهذا لا يحدث لان الأجسام لا تصل ابداً إلى سرعة الضوء، كما أن فوتونات الضوء تتحرك بسرعة الضوء ولكن كتلتها لا تساوى مالانهاية وكتلتها وهي متحركة تساوى حاصل ضرب مالانهاية x صفر فكتلتها الحركية تساوي قيمة معينة لاصفرية وليست مالانهاية لان الفوتونات هي كمات من الطاقة وكتلتها تساوى صفر في حالة السكون فقط

انظر أيضاً

• تجربة ميكلسون ومورلي
• تقلص الأطوال
• إبطاء زمني
• معادلات آينشتين للمجال
• نظرية النسبية الخاصة
• نظرية النسبية العامة
• سرعة الضوء
• تأثير ساغناك
• نسبية التزامن
• زمكان
• تحويل جاليليو
• مبدأ النسبية