تجربة تروتون ونوبل

تجربة تروتون-نوبل- هي عبارة عن تجربة اكتشاف حركة الأرض من خلال الأثير الناقل للضوء، وقد أجريت هذه التجربة في عامي 1901 – 1903م، عن طريق كل من: فريدريك توماس تروتون، وهـنري.ر. نوبل. والتجربة كانت تقوم على اقتراح الفيزيائي الأيرلندي، جورج فيتزجيرالد، بأن المكثف المشحون ذو اللوحين المتوازيين المتحرك عبر الأثير، يجب أن يوجه نفسه بشكل عمودي على الحركة. وكما حدث في تجربة مايكلسون- مورلي السابقة، حصل تروتون ونوبل على نتيجة صفرية مؤداها: لا يمكن اكتشاف أي حركة بالنسبة للأثير. وتم إعادة إنتاج هذه النتيجة الصفرية، من خلال رودولف توماشيك (1925، 1926)، وتشيس (1926، 1927)، وهايدن في عام 1994. ومثل هذه النتائج التجريبية، المتسقة مع النسبية الخاصة، يُنظر إليها الآن على أنها تعكس صحة مبدأ النسبية. والتجربة هي عبارة عن اختبار للنسبية الخاصة.

مكثف دائري B ، قطره 7.7 سم، مصنوع من طبقات متعددة من الميكا ورقائق القصدير ، تم تركيبه في كرة سيلولويد كروية ناعمة D مغطاة بطلاء موصل، ومعلقة بسلك ناعم من البرونز الفسفوري بطول 37 سم داخل أنبوب مؤرض. تم توصيل السلك بأحد أقطاب آلة Wimshurst التي تحافظ على لوحات متناوبة من المكثف مشحونة إلى 3000 فولت. تم الحفاظ على اللوحات المقابلة للمكثف وكذلك كرة السليولويد عند جهد أرضي بواسطة سلك من البلاتين تم غمسه في حمام حمض الكبريتيك الذي لم يعمل فقط كقطب موصل، بل عمل أيضًا على تخميد التذبذبات وعمل كمجفف . تمت رؤية المرآة المرفقة بالمكثف من خلال تلسكوب وسمحت برؤية التغييرات الدقيقة في الاتجاه.

وترتبط تجربة تروتون-نوبل أيضًا بتجارب فكرية أخرى، مثل "مفارقة تروتون- نوبل"، و"رافعة الزاوية القائمة" أو "مفارقة لويس-تولمان". وثمة العديد من الحلول، التي تم طرحها لحل هذا النوع من المفارقات، وجميعها يتفق مع النسبية الخاصة.

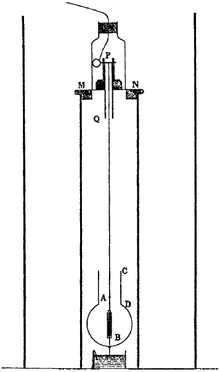
تجربة تروتون- نوبل

في هذه التجربة، يتم تثبيت مكثف معلق ذو لوحين متوازيين بواسطة ألياف الالتواء الدقيقة ويتم شحنه. وإذا كانت نظرية الأثير صحيحة، فإن التغيير في معادلات ماكسويل بسبب حركة الأرض عبر الأثير سوف يؤدي إلى عزم دوران يتسبب في محاذاة الصفائح بشكل عمودي على الحركة. ويتم تقديم ذلك من خلال التالي:

$\tau =-E'{\frac {v^{2}}{c^{2}}}\sin 2\alpha '$

حيث $\tau$ هي عزم الدوران، $E$ هي طاقة المكثف، $\alpha$ تمثل الزاوية بين العمودي للوحة والسرعة.

ومن جانب آخر، فإن تأكيد النسبية الخاصة على أن معادلات ماكسويل ثابتة لجميع الأطر المرجعية المتحركة بسرعات ثابتة، من شأنه أن يتنبأ بعدم وجود عزم دوران (نتيجة صفرية). وهكذا، إذا لم يكن الأثير ثابتًا بطريقة ما بالنسبة للأرض، فإن التجربة هي اختبار لمعرفة أي من هذين الوصفين هو الأكثر دقة. وعليه فإن نتيجتها الصفرية تؤكد على مقياس لورنتز للنسبية الخاصة.

ومع ذلك، وفي حين أن النتيجة التجريبية السلبية، يمكن تفسيرها بسهولة في إطار السكون للجهاز، فإن التفسير من وجهة نظر إطار غير متحرك (فيما يتعلق بالسؤال، ما إذا كان ينبغي أن ينشأ نفس عزم الدوران كما هو الحال في "الإطار الأثيري" الموصوف أعلاه، أو عدم ظهور عزم الدوران على الإطلاق) هو أمر أكثر صعوبة، ويسمى "مفارقة تروتون- نوبل"، والتي يمكن حلها بعدة طرق (انظر الحلول أدناه).

مفارقة الرافعة ذات الزاوية القائمة

تعادل مفارقة تروتون- نوبل بشكل أساسي تجربة فكرية أخري تسمى مفارقة الرافعة القائمة، والتي تمت مناقشتها للمرة الأولي من قبل جيلبرت نيوتن لويس وريتشارد تشيس تولمان في عام 1909م. لنفترض رافعة قائمة الزاوية بنقاط النهاية abc. في إطار السكون، القوى

𝑓𝑦 أتجاه ba، و 𝑓𝑥 أتجاه bc

يجب أن تكون متساوية للحصول على التوازن، وبالتالي لا يعطي قانون الرافعة أي عزم دوران:

$\tau '=L_{0}\left(f'_{x}-f'_{y}\right)=0$

حيث $\tau$ هي عزم الدوران، و $L_{0}$ الطول المتبقي من ذراع الرافعة الواحدة. ومع ذلك، وبسبب انكماش الطول، فإن ba أطول من bc في نظام غير متحرك، وبالتالي فإن قانون الرافعة يعطي:

$\tau =f_{x}\cdot L_{0}-f_{y}\cdot L_{0}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}=L_{0}\left(f_{x}-f_{y}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}\right)$

ويمكن ملاحظة أن عزم الدوران ليس صفرًا، مما قد يتسبب على ما يبدو في دوران الرافعة في الإطار غير المتحرك. ونظرًا لعدم ملاحظة أي دوران، فقد استنتج لويس وتولمان، أنه لا يوجد عزم دوران، وبالتالي:

${\frac {f_{x}}{f_{y}}}={\sqrt {1-{\frac {v^{2}}{c^{2}}}}}$

ومع ذلك، وكما أوضح ماكس فون لاو (1911م)، فإن هذا يتناقض تمامًا مع التعبيرات النسبية الخاصة بالقوة،

$f_{x}=f'_{x},\ f_{y}=f'_{y}\cdot {\sqrt {1-{\frac {v^{2}}{c^{2}}}}}$

الذي يعطي

${\frac {f_{x}}{f_{y}}}={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$

وعندما يتم تطبيق ذلك على قانون الرافعة، يتم إنتاج عزم الدوران التالي:

$\tau =-L_{0}\cdot f'_{x}\cdot {\frac {v^{2}}{c^{2}}}$

وهي في الأساس نفس المشكلة الموجودة في مفارقة تروتون- نوبل.

الحلول

إن عملية التحليل النسبي التفصيلي لكل من مفارقة تروتون- نوبل، ومفارقة الرافعة ذات الزاوية القائمة تتطلب الحرص على التوفيق بشكل صحيح، على سبيل المثال، التأثيرات التي يراها المراقبون في أطر مرجعية مختلفة، ولكن يظهر في النهاية أن كل هذه الأوصاف النظرية تعطي النتيجة نفسها. في كلتا الحالتين، لا يؤدي عزم الدوران الصافي الظاهرعلى جسم ما (عند النظر إليه من إطار مرجعي معين) إلى أي دوران للجسم، وفي كلتا الحالتين يتم تفسير ذلك من خلال الحساب الصحيح، بالطريقة النسبية، لتحويل جميع القوى ذات الصلة، والزخم، والتسارع الناتج عنها. وقد تم مراجعة التاريخ المبكر لوصف هذه التجربة عن طريق جانسن (1995).

التيار الحالي

تم تقديم الحل الأول لمفارقة تروتون- نوبل من خلال هندريك لورينتز (1904م). وتعتمد نتيجته على افتراض أن عزم الدوران، والزخم الناتج عن القوى الكهروستاتيكية يتم تعويضهما بعزم الدوران والزخم الناتجين عن القوى الجزيئية. ومع ذلك، فليس هناك آلية محددة لكيفية قدرة إنتاج تحويل لورنتز لمثل هذه القوى الجزيئية. بالإضافة إلى أنه، إذا كانت الشحنات ذات النقطتين متصلة بسلسلة مرنة، فلن تتمكن أي قوة جزيئية من إنتاج عزم دوران.

وقد تم توضيح ذلك بشكل أكثر تفصيلاً من قبل ماكس فون لاو (1911م)، الذي أعطى الحل القياسي لهذا النوع من المفارقات. والذي استند فيه إلى ما يسمى " بتكافؤ الكتلة والطاقة " في صياغتها العامة بواسطة ماكس بلانك. ووفقًا لماكس فون، يتم إنتاج تيار طاقة مرتبط بزخم معين ("تيار لاوي") في الأجسام المتحركة بواسطة الضغوط المرنة. إن عزم الدوران الميكانيكي الناتج في حالة تجربة تروتون-نوبل يساوي:

$\tau =E'{\frac {v^{2}}{c^{2}}}\sin 2\alpha '$

وفي ذراع الزاوية القائمة:

$\tau =L_{0}\cdot f'_{x}\cdot {\frac {v^{2}}{c^{2}}}$

والذي يعوض بشكل تام عزم الدوران الكهرومغناطيسي المذكور أعلاه، وبالتالي لا يحدث دوران في كلتا الحالتين. أو بعبارة أخرى: إن عزم الدوران الكهرومغناطيسي ضروري فعليًا للحركة المنتظمة للجسم، أي لمنع الجسم من الدوران بسبب عزم الدوران الميكانيكي الناتج عن الضغوط المرنة.

ومنذ ذلك الحين، ظهرت العديد من الأوراق البحثية التي تناولت تيار لاو بشكل أكثر تفصيلاً، وقدمت بعض التعديلات أو إعادة التفسير، وتضمنت متغيرات مختلفة للزخم "الخفي".

القوة والتسارع

لقد تم نشر حل بدون قوى تعويضية، أو إعادة تعريف للقوة والتوازن، وذلك عن طريق كل من: ريتشارد تولمان وبول سوفوس إبستاين في عام 1911م. فقد طبقوا مفهوم الكتلة النسبية التي تختلف في الأتجاهين الطولي والعرضي بحيث لا يكون للقوة والتسارع نفس الاتجاه دائمًا. والدور الذي يلعبه مفهوم القوة في النسبية يختلف كثيرًا عن دور ميكانيكا نيوتن. وقد توصل فرانكلين (2006م) إلى استنتاج مماثل من خلال استخدام كتلة ثابتة لا تتغير مع الاتجاه، ولكن باستخدام حقيقة أن اتجاه التسارع النسبي يختلف عن اتجاه القوة النسبية.

وقد تخيل إبستاين عصا عديمة الكتلة بنهايتي OM ، مثبتًة عند النقطة O، وجسيمًا ذو كتلة سكون "m" مثبتًا عند النقطة M. تشكل العصا الزاوية $\tan \alpha '$ مع المحور y. الآن قوة $f'$ يتم تطبيقه نحو O عند M ، ويتم تحقيق التوازن في إطار السكون الخاص به عندما ${\tfrac {f'_{x}}{f'_{y}}}=\tan \alpha '$ . وكما هو موضح أعلاه، فإن هذه القوى في إطار غير متحرك تأخذ الشكل:

$f_{x}=f'_{x},\ f_{y}=f'_{y}\cdot {\sqrt {1-{\frac {v^{2}}{c^{2}}}}},\ \tan \alpha =\tan \alpha '{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}$

هكذا ${\frac {f_{x}}{f_{y}}}={\frac {\tan \alpha }{1-{\frac {v^{2}}{c^{2}}}}}$ .

لذلك فإن القوة المحصلة لا تتجه مباشرة من "O" إلى "M". وهل يؤدي هذا إلى دوران العصا؟ لا، لأن إبستاين أخذ في الاعتبار التسارع الناتج عن القوتين. واستخدم مفهوم الكتلة النسبية التي تختلف في الاتجاه الطولي والاتجاه العرضي بحيث

$m_{\rm {long.}}={m_{0}\gamma ^{3}},\ m_{\rm {tr.}}=m_{0}\gamma ,\quad {\rm {where}}\quad \gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$ .

إن التعبيرات النسبية في الحالة التي تتسارع فيها كتلة "m" بواسطة هاتين القوتين في الاتجاه الطولي والعرضي، تتمثل في:

$a_{x}={\frac {f_{x}}{m\gamma ^{3}}},\ a_{y}={\frac {f_{y}}{m\gamma }}$ .

هكذا ${\frac {a_{x}}{a_{y}}}=\tan \alpha$ .

واستخدم فرانكلين العلاقة النسبية بين القوة والتسارع،

${\frac {d{\bf {p}}}{dt}}=m{\frac {d}{dt}}({\bf {v}}\gamma )=m\gamma ^{3}[{\bf {a}}+{\bf {v\times (v\times a)}}].$

ومن خلال استخدام هذه العلاقة بين القوة النسبية والتسارع، يمكن إثبات عدم حدوث دوران في هذا النظام. ويجب تطبيق اعتبارات مماثلة أيضًا على كل من: رافعة الزاوية القائمة، ومفارقة تروتون- نوبل. وهكذا يتم حل المفارقات، لأن التسارعين (بوصفهما متجهين) يشيران إلى مركز ثقل النظام، على الرغم من أن القوتين لا تشيران إلى ذلك.

انظر أيضًا

• تاريخ النسبية الخاصة.
• تجربة مايكلسون- مورلي.