آلة الفائدة الميكانيكية
آلة الفائدة الميكانيكية أو آلة الفائدة الحراكية وتسمى الآلة البسيطة التي تعرض الـ فائدة الميكانيكية على سبيل المثال:
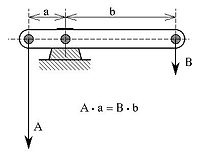
- رافعة: الكمرة المعروضة في توازن غير متحرك حول نقطة الارتكاز. وهذا نتيجة العزم الذي تنتجه القوة الموجهة "أ" عكس حركة اتجاه عقارب الساعة (العزم أ*أ) في التوازن الذي أنتجته القوة الموجهة "B" في اتجاه حركة عقارب الساعة (عزم ب*ب). فالقوة الموجهة النسبية المنخفضة "ب" تنعكس في القوة الموجهة العالية نسبيًا "A". ومن ثمّ تزيد القوة في النسبة بين القوتين أ : ب والتي تساوي نسبة المسافات بين نقطتي ارتكاز ب : أ. فهذه النسبة تسمى الفائدة الميكانيكية. وهذا الموقف النموذجي لا يهتم بالاحتكاك.
- حركة الملفاف ذو الدولاب والجزع (على سبيل المثال المفكات ومقابض الأبواب): يعتبر الملفاف في الأساس رافعة مزودة بذراع يمثل المسافة بين المحور والنقطة الخارجية للملفاف، والآخر نصف قطر المحور. ونموذجيًا يعتبر هذا فرقًا كبيرًا تامًا يؤدي إلى فائدة ميكانيكية تناسبية كبيرة. وهذا يتيح للملفافات البسيطة ذات المحاور الخشبية التي تدور في القوالب الخشبية أن تستمر في الدوران بحرية، وهذا لأن الاحتكاك تعوقه قوة الدوران للملفاف مضروبة في الفائدة الميكانيكية.
- البكارة متعددة البكرات تنتج فائدة ميكانيكية من خلال المادة المرنة المعقودة على العديد من البكرات في مقابل ذلك. ويمكن الحصول على المزيد من الفائدة الميكانيكية بإضافة المزيد من العقد والبكرات.
- مرود: يعتبر المرود سطحًا منحدرًا يُلف حول أسطوانة. فالمرور على أعلى هذا المسطح المنحدر يعتبر الفائدة الميكانيكية للمرود.[1]
البكرات
عدليهتم برفع الأثقال باستعمال الحبل والبكرات. فيتم لف الحبل حول البكرة المتصلة بنقطة ثابتة على سبيل المثال عارضة سطح مخزن، والاتصال بالوزن يسمى بكرة مفردة. لديها فائدة ميكانيكية = 1 (مع افتراض عدم وجود مراكز احتكاك في البكرة)، بما يعني عدم وجود فائدة ميكانيكية (أو عيب) إلا أنه ربما يكون تغيير الاتجاه منتجًا للفائدة.
تحتوي البكرة المتحركة المفردة على فائدة ميكانيكية تساوي 2 (مع افتراض عدم وجود مراكز احتكاك في البكرة) تأمل رفع ثقل من خلال بكرة متصلة به. فالحبل يدور حولها حيث يتصل أحد الأطراف بنقطة ثابتة في الأعلى، على سبيل المثال عارضة سطح مخزن، ويتم الرفع بقوة إلى أعلى من الطرف الآخر حيث يتوازى الطولان. ففي هذا الحالة تصبح المسافة التي ينبغي على أداة الرفع جذب الحبل خلالها ضعف المسافة التي ينتقل خلالها الوزن مما يجعل القوة المستخدمة تنتصف. لاحظ: إذا تم استخدام بكرة إضافية لتغيير اتجاه الحبل، على سبيل المثال كأن يريد الشخص الذي يقوم بالعمل الوقوف على الأرض بدلًا من العارضة، فإن الفائدة الميكانيكية لا تزيد.
وبلف المزيد من الحبال حول المزيد من البكرات، يمكن أن نستمر في زيادة الفائدة الميكانيكية. على سبيل المثال، إذا كان لدينا بكرتان متصلتان بالعارضة، وبكرتان متصلتان بالوزن، وأحد الأطراف متصل بالعارضة وأحد الأفراد يقف على العارضة الجاذبة للحبل؛ فلدينا فائدة ميكانيكية تساوي أربعة. ولاحظ مجددًا: إذا أضفنا بكرة أخرى حتى يقف شخص آخر على الأرض ويجذب إلى أسفل فسيستمر الحصول على فائدة ميكانيكية تساوي أربعة.
وفيما يلي أمثلة حيث لم تكن النقطة الثابتة واضحة:
- قفل على هيئة سوار بحذاء يمر من فتحة ثم ينحني على نفسه. تعتبر الفتحة بكرة متحركة والفائدة الميكانيكية = 2.
- حبلان ملقيان على سلم متصل بمنصة. وتم ربط الحبلين على برميل ثم مر الحبلان على البرميل وأخذهما عاملان أعلى السلم. ويسحب العاملان الحبلين معًا لرفع البرميل إلى أعلى. فالبرميل يعتبر بكرة متحركة والفائدة الميكانيكية = 2، وإذا وجد احتكاك مناسب حيث يضغط على الحبل بين البرميل والسلم، فإن نقطة الضغط تصبح نقطة التعلق. وتعتبر هذه نقطة تعلق ثابتة لأن الحبل فوق البرميل لا يتحرك في تناسب مع السلم. ولكن بدلًا من ذلك يمكن تثبيت أطراف الحبل بالمنصة.
- الكتلة والمرفاع: الفائدة الميكانيكية = 2 أو أكثر، بناء على التصميم (انظر أعلاه)
المراود
عدليمكن حساب الفائدة الميكانيكية النظرية للمرود بتطبيق المعادلة التالية:[2]
حيث
- dm = متوسط قطر دائرة حبل المرود
- l = المركز الأمامي بحبل المرود
لاحظ أن الفائدة الميكانيكية الفعلية لـنظام المرود تعتبر أكبر، حيث إن محرك المرود أو نظام تحريك المرود لديه فائدة ميكانيكية أيضًا.
- مستوى منحدر: الفائدة الميكانيكية = طول المنحدر ÷ ارتفاع المنحدر
انظر أيضًا
عدلمراجع
عدلوصلات خارجية
عدل- Gears and pulleys
- Mechanical engineering — pulleys
- Mechanical advantage — video
- How to Dunk a Doughnut: The Science of Everyday Life، Arcade Publishing، 2003، ISBN:978-1-55970-680-3، مؤرشف من الأصل في 2019-12-08
{{استشهاد}}: الوسيط|الأول=يفتقد|الأخير=(مساعدة) - Basic machines and how they work (ط. Revised 1994)، Courier Dover Publications، 1971، ISBN:978-0-486-21709-3، مؤرشف من الأصل في 2019-12-08